There are no products in the cart!
-
15 Tháng 09, 2021
-
3495 views
Các lệnh trong ngôn ngữ R - Kiểm định cơ bản trong R
Chào các độc giả, sau đây MOSL xin phép giới thiệu các bạn các lệnh trong ngôn ngữ R cũng như các kiểm định cơ bản trong phần mềm này.
[toc]
1. Các lệnh trong ngôn ngữ R
Trước hết chúng ta yêu cầu R nhập bộ dữ liệu ch2_health.wf1 dưới dạng một data.frame tên mới là dung đồng thời chỉ định R chỉ làm việc với file dữ liệu này như sau:

1.1. Thống kê mô tả trong R
Thống kê mô tả sơ bộ cho các biến số trong bộ dữ liệu:
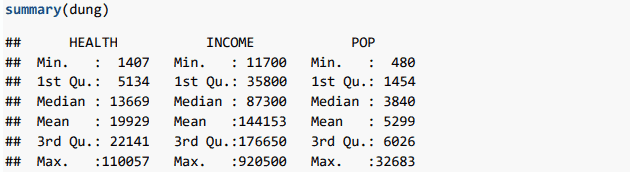
Chúng ta có kết quả hoàn toàn tương tự với toán tử pipe:

Nếu chúng ta quan tâm đến các chi tiết thống kê chi tiết hơn cho bộ số liệu chúng ta có thể sử dụng gói pastecs:
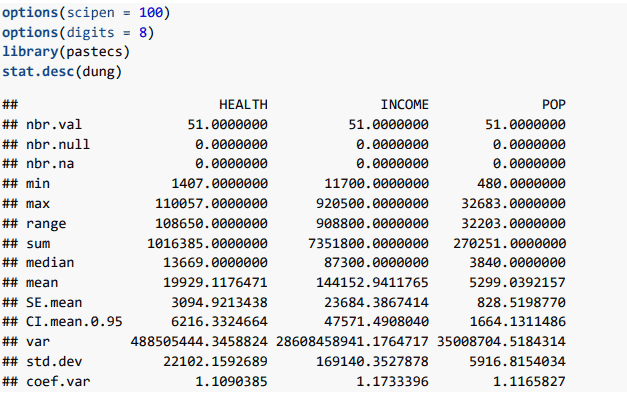
- Quãng đáng tin 95% của HEALTH nằm trong khoảng từ 19929 – 6216 đến 19929 + 6216.
- Còn giá trị coef.var = 1.109 chính là thương số của std.dev chia cho mean.
- Giá trị (CI.mean.0.95) là quãng đáng tin 95% cho các biến số
Chú ý: (CI là viết tắt của chữ Confidence Interval – quãng đáng tin).
1.2. Ma trận hệ số tương quan
Ma trận hệ số tương quan giữa các biến số:

Hệ số tương quan giữa POP và INCOME gần bằng 1 (lớn hơn 0.8) nên nếu cả hai biến này xuất hiện với tư cách là biến độc lập trong phương trình hồi quy thì mô hình có thể mắc lỗi đa cộng tuyến ở mức độ nghiên trọng.
2. Một số kiểm định cơ bản trong R
Mục này chúng ta xem xét việc thực hiện hồi quy đơn cũng như thực hiện các kiểm định thường gặp với R.
2.1. Hồi quy đơn, khoảng tin cậy cho các hệ số và bảng ANOVA
Chúng ta xét mô hình hồi quy hai biến số sau:
HEALTH = β1 + β2INCOME. + ui (1)
Để ước lượng mô hình này trong R:

Các bạn có thể nâng độ chính xác của các kết quả bằng cách thêm lệnh như sau:

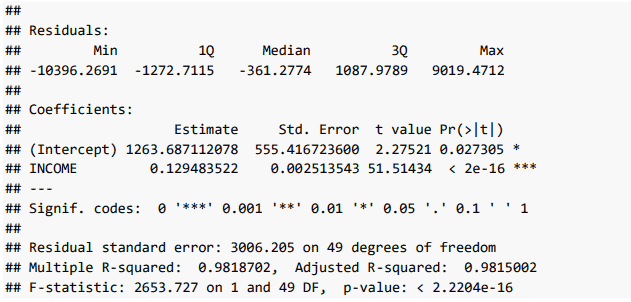
Lúc này, thống kê F được lấy tới 3 chữ số sau dấu phẩy.
Rõ ràng, nếu căn cứ theo các tiêu chuẩn truyền thống thì mô hình hồi quy của chúng ta là tốt thể hiện ở:
- (1) tất cả các hệ số hồi quy có ý nghĩa thống kê ở mức 5%,
- (2) R2 rất cao
- (3) thống kê F có giá trị lớn.
Sau khi thực hiện hồi quy chúng ta có thể sử dụng một số hàm để khai thác thêm một số thông tin liên quan đến mô hình.
Dưới đây là một số hàm cơ bản:
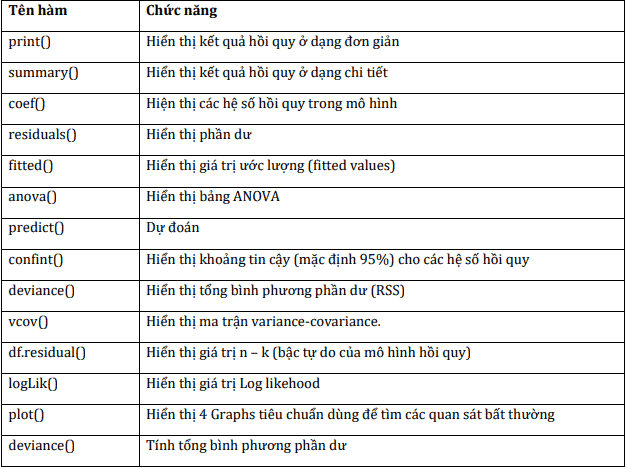
Bên cạnh đó, nhằm hỗ trợ cho việc chẩn đoán các lỗi của mô hình (hiện tượng đa cộng tuyến, phương sai sai số thay đổi, các quan sát bất thường) – một vấn đề mà chúng ta sẽ nghiên cứu kĩ hơn trong các phần sau của tài liệu này.
Sau khi thực hiện hồi quy chúng ta có thể sử sụng một số hàm mà gói car cung cấp dưới đây:


2.1.1. Tính khoảng tin cậy trong R
Phần trên chúng ta đã quen thuộc với hàm summary(). Phần này sẽ đi vào mức ý nghĩa và độ tin cậy trong R.
Chẳng hạn để tính khoảng tin cậy 95% cho các hệ số hồi quy:

Tính khoảng tin cậy 90% cho các hệ số hồi quy:

2.1.2. Giá trị F trong kiểm định Anova trong phần mềm R
Một trong những thông tin quan trọng khi thực hiện hồi quy là phân tích bảng ANOVA:
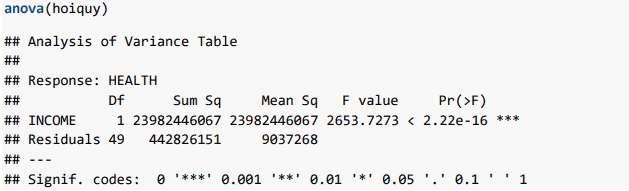
Ở đây RSS (với df2 = 51 – 2 = 49 bậc tự do) là 442826151 và ESS (với df1 = 1 bậc tự do) là 23982446067. Với chú ý rằng TSS = RSS + ESS chúng ta có thể kiểm tra lại là R2 =ESS/TSS = 0.982.
Bảng ANOVA này cũng hiển thị giá trị thống kê F là 2653.727 = (ESS/df1)/(RSS/df2) = (23982446067/1)/( 442826151/49).
Kết quả này chính là giá trị F được hiển thị ở kết quả phân tích hồi quy.
- Trong tình huống chúng ta muốn thực hiện ước lượng cho mô hình:
HEALTH = β1 + β2INCOME^2+ u
Do mỗi một phần mềm đều có một quy cách thực hiện nên trong R bạn phải gõ:

Một tình huống khác mà chúng ta có thể gặp là thực hiện hồi quy không có hệ số chặn (Regression through the Origin).
- Đó là các mô hình hồi quy dạng:
HEALTH = β⨉INCOME + u
- Thực hiện hồi quy không có hê số chặn cho mô hình trên trong R là:

Chú ý rằng trong hồi quy không có hệ số chặn thì chỉ tiêu R2 được tính theo công thức truyền thống là không áp dụng được và không có ý nghĩa trong việc đánh giá độ phù hợp của mô hình.
Chúng ta sẽ nghiên cứu kĩ hồi quy không có hệ số chặn trong chương sau.
2.2. Kiểm định Jarque – Bera Test cho tính phân phối chuẩn của phần dư
Kiểm định tính phân phối chuẩn của phần dư (hay bất kì biến số này khác) có thể được thực hiện bằng nhiều test khác khau.
2.2.1. Kiểm định Jarque – Bera Test
Chẳng hạn chúng ta có thể thực hiện kiểm định Jarque – Bera Test cho tính phân phối chuẩn của phần dư.
Thống kê JB này tuân theo phân phối khi bình phương (χ2) với hai bậc tự do.
- Nếu giá trị JB tính toán ứng với p-value lớn hơn 5% thì chúng ta chưa thể bắc bỏ giả thiết rằng phân phối là chuẩn.
- Ngược lại, ta chấp nhận giả thuyết phân phối là không chuẩn.
Phân tích hình ảnh có thể chỉ cho ta thấy rằng phần dư có thể là phân phối chuẩn hay không:

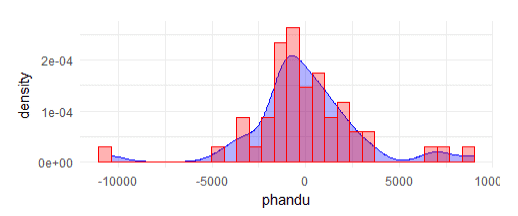
Hoặc có thể thể hiện bằng line graph như phần mềm Eviews thường thực hiện:
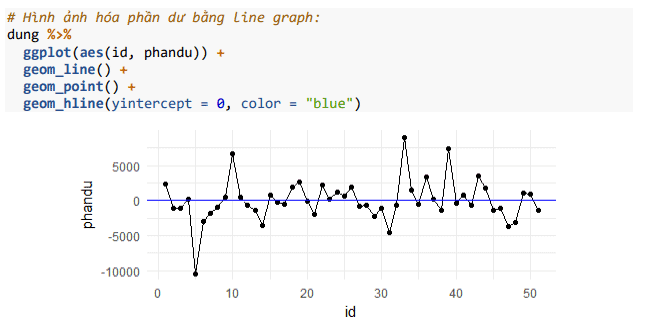
Những hình ảnh trên không chỉ ra dấu hiệu chắc chắn nào cho thấy phần dư là phân phối chuẩn.
Chúng ta có thể sử dụng kiểm định Jarque – Bera để đưa ra bằng chứng thống kê về phân phối chuẩn:
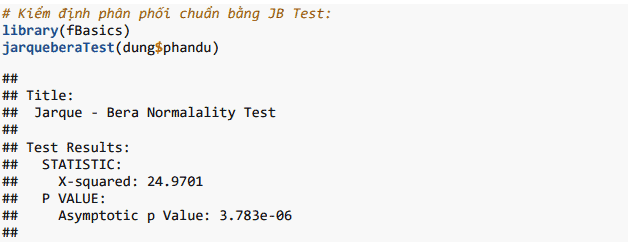
Giá trị của Asymptotic p Value = 3.783*10-6 > 5% nên chúng ta có bằng chứng thống kê để chấp nhận giả thuyết gốc rằng phần dư phân phối chuẩn.
Vì các thông tin về phần dư là rất quan trọng trong việc chẩn đoán các lỗi của mô hình hồi quy – một vấn đề mà chúng ta sẽ nghiên cứu chi tiết từ chương 7 nên chúng ta nên lưu các giá trị phần dư này để sử dụng và gán nó vào data frame tên dung như ở trên.
2.2.2. Đánh giá chi tiết về phần dư
Chúng ta cũng có thể đánh giá chi tiết hơn về phần dư thu được:
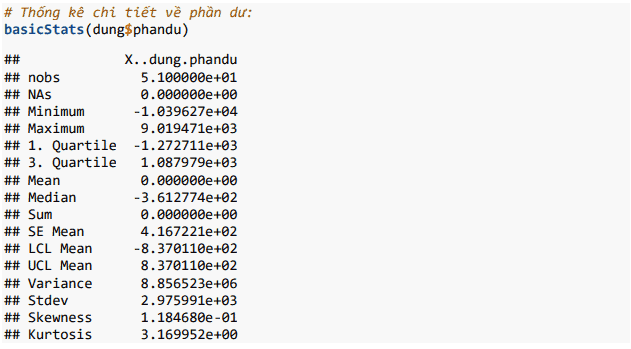
Chúng ta thấy rằng phần dư có Mean = 0, Skewness = 0.118 (độ méo), và Kurtosis = 3.169.
Những thông tin này ngụ ý rằng phần dư có thể không phân phối chuẩn. Và kiểm định Jarque-Bera mà chúng ta thực hiện ở trên đã đưa ra bằng chứng thống kê cho nhận định trên.
Cũng có thể thực hiện kiểm định giả thiết rằng các hệ số hồi quy thu được phân phối chuẩn hay không với kiểm định Jarque – Bera Normalality Test sử dụng gói fBasics:

Các giá trị P-value đều lớn hơn 5% nên chúng ta có bằng chứng thống kê cho thấy phân phối của các hệ số beta là chuẩn.
2.3. Kiểm định Durbin – Watson
Trong Eviews mỗi khi chạy hồi quy thì mặc định xuất hiện giá trị của Durbin-Watson Test – một kiểm định thường dùng đến khi đánh giá hiện tượng tự tương quan (Autocorrelation) – một vấn đề về lỗi mô hình rất phổ biến với chuỗi dữ liệu thời gian với cặp giả thuyết sau:
- H0: Phần dư của mô hình không có tự tương quan
- H1: Phần dư của mô hình có tự tương quan
Nếu cần thiết, trong R cũng có thể thực hiện kiểm định này với gói lmtest bằng hàm dwtest():
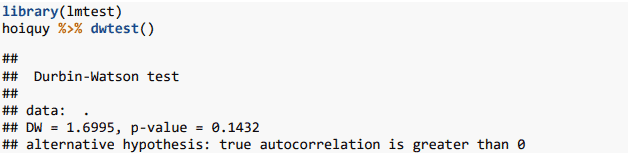
Căn cứ vào giá trị p-value = 0.143 > 5% chúng ta có thể chấp nhận giả thuyết gốc rằng không tồn tại tự tương quan trong mô hình.
Cũng cần phải lưu ý rằng kiểm định Durbin – Watson có khả năng áp dụng rất hạn chế vì kiểm định này chỉ áp dụng cho tương quan bậc 1 và mô hình không có biến nội sinh.
2.4. Kiểm định Wald cho 1 hệ số hồi quy
Giả sử chúng ta tin rằng số hồi quy β2 = 0.15. Chúng ta có thể kiểm định giả thuyết này với gói AER như sau:

Cột giá trị Pr(>F) = 10.79⨉10-11 là rất bé nên ta bác bỏ giả thiết β2 = 0.15.
Bạn có thể thực hiện kiểm định này bằng gõ linear.hypothesis(hoiquy,”INCOME=0.15″).
Tất nhiên kết quả là không thay đổi.
2.5. Kiểm định Wald cho nhiều hệ số hồi quy
Nếu chúng ta tin rằng β1 = 1300 và β2 = 0.15 chúng ta có thể thực hiện kiểm định Wald như sau:
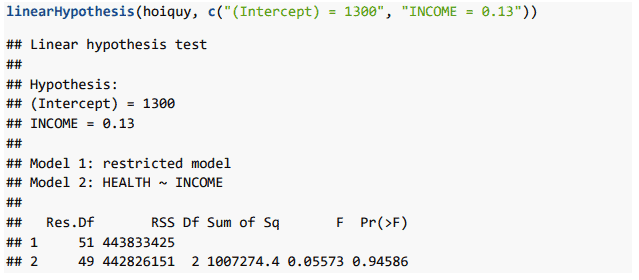
Cột giá trị Pr(>F) = 0.94 > 5% nên chúng ta có bằng chứng thống kê cho rằng β1 = 1300 và β2 = 0.15.
Ở đây các bạn cần chú ý rằng mặc dù chúng ta bắc bỏ giả thuyết β2 = 0.15 (mục 4.5) nhưng chúng ta lại chấp nhận giả thuyết rằng β1 = 1300 và β2 = 0.15.
5. Kết luận
Dưới đây là các lệnh trong ngôn ngữ R và một số kiểm định cơ bản trong phần mềm này.
Cuối bài MOSL xin chúc các độc giả học tập và làm việc hiệu quả.
Xem thêm: Dịch vụ chạy R của Mosl.vn
Liên hệ:
Hotline: 0707.33.9698 hoặc Mail: sales@mosl.vn | Fanpage: Mentor Of Số Liệu – Mosl.vn
Tag:
Nguồn: Tác giả Nguyễn Chí Dũng













