There are no products in the cart!
-
04 Tháng 01, 2022
-
3009 views
Mô hình Logit & Probit – Logistic Regression in Stata
Hồi quy logistic là gì? Hồi quy Logistic (Logistic Regression) trong phân tích thống kê (hay còn được gọi là mô hình logit) là phân tích hồi quy thích hợp để tiến hành khi biến phụ thuộc là nhị phân (lưỡng phân), nói cách khác là hồi quy với biến phụ thuộc bị giới hạn (Limited Dependent Variable Models).
Bài viết này Mosl sẽ hướng dẫn các bạn khái niệm về hồi quy logistic là gì? cùng với các mô hình đi kèm cùng cách chạy trong phần mềm Stata.
1. Logistic Regression – Mô hình Logit là gì?
1.1. Khái niệm

[su_quote cite=”MOSL” url=”mosl.vn”] Hồi quy logistic (Logistic Regression) trong phân tích thống kê (hay còn được gọi là mô hình logit) là phân tích hồi quy thích hợp để tiến hành khi biến phụ thuộc là nhị phân (lưỡng phân), nói cách khác là hồi quy với biến phụ thuộc bị giới hạn (Limited Dependent Variable Models). Giống như tất cả các phân tích hồi quy, hồi quy logistic là một phân tích dự đoán. Hồi quy logistic được sử dụng để mô tả dữ liệu và giải thích mối quan hệ giữa một biến nhị phân phụ thuộc và một hoặc nhiều biến độc lập cấp danh nghĩa, thứ tự, khoảng hoặc tỷ lệ. [/su_quote]
[su_quote cite=”https://en.wikipedia.org/wiki/Logistic_regression” url=”mosl.vn”] Hồi quy logistic (Logistic Regression) là một mô hình thống kê ở dạng cơ bản của nó sử dụng một hàm logistic để mô hình hóa một biến phụ thuộc nhị phân , mặc dù tồn tại nhiều phần mở rộng phức tạp hơn . Trong phân tích hồi quy , hồi quy logistic (hay hồi quy logit ) là ước lượng các tham số của mô hình logistic (một dạng của hồi quy nhị phân ). Về mặt toán học, mô hình logistic nhị phân có một biến phụ thuộc với hai giá trị có thể có, chẳng hạn như đạt hoặc không đạt được đại diện bởi một biến chỉ báo, trong đó hai giá trị được gắn nhãn “0” và “1”. [/su_quote]
1.2. Ví dụ
Loại phân tích này có thể giúp bạn dự đoán khả năng xảy ra một sự kiện hoặc một lựa chọn được đưa ra.
Ví dụ: Bạn có thể muốn biết khả năng khách truy cập chọn một ưu đãi được thực hiện trên trang web của bạn – hay không (biến phụ thuộc). Phân tích của bạn có thể xem xét các đặc điểm đã biết của khách truy cập, chẳng hạn như các trang web họ đến, lượt truy cập lặp lại vào trang web của bạn, hành vi trên trang web của bạn (các biến độc lập).
Mô hình hồi quy logistic giúp bạn xác định xác suất loại khách truy cập có khả năng chấp nhận đề nghị hay không. Do đó, bạn có thể đưa ra quyết định tốt hơn về việc quảng cáo phiếu mua hàng của mình hoặc đưa ra quyết định về chính phiếu mua hàng đó.
1.3. Ưu nhược điểm của Logistic Regression
Đến đây, hy vọng bạn đã có một ý tưởng rõ ràng hơn nhiều về hồi quy logistic là gì và các loại kịch bản mà nó có thể được sử dụng. Bây giờ chúng ta hãy xem xét một số ưu điểm và nhược điểm của loại phân tích hồi quy.
Ưu điểm
- Hồi quy logistic dễ thực hiện hơn nhiều so với các phương pháp khác, đặc biệt là trong Machine Learning: Mô hình Machine Learning có thể được mô tả như một mô tả toán học của một quá trình trong thế giới thực. Quá trình thiết lập mô hình học máy yêu cầu đào tạo và thử nghiệm mô hình. Huấn luyện là quá trình tìm kiếm các mẫu trong dữ liệu đầu vào, để mô hình có thể ánh xạ một đầu vào cụ thể (ví dụ, một hình ảnh) tới một loại đầu ra nào đó, chẳng hạn như một nhãn. Hồi quy logistic dễ đào tạo và triển khai hơn so với các phương pháp khác.
- Hồi quy logistic hoạt động tốt đối với các trường hợp tập dữ liệu có thể phân tách tuyến tính: Tập dữ liệu được cho là có thể phân tách tuyến tính nếu có thể vẽ một đường thẳng có thể tách hai lớp dữ liệu khỏi nhau. Hồi quy logistic được sử dụng khi biến Y của bạn chỉ có thể nhận hai giá trị và nếu dữ liệu có thể phân tách tuyến tính, thì việc phân loại nó thành hai lớp riêng biệt sẽ hiệu quả hơn.
- Hồi quy logistic cung cấp những hiểu biết hữu ích: Hồi quy logistic không chỉ cho phép đo lường mức độ liên quan của một biến độc lập (tức là (kích thước hệ số), mà còn cho chúng ta biết về hướng của mối quan hệ (tích cực hoặc tiêu cực). Hai biến được cho là có một liên kết tích cực khi sự gia tăng giá trị của một biến số cũng làm tăng giá trị của biến số khác. Ví dụ: bạn càng dành nhiều giờ tập luyện, bạn càng trở nên giỏi hơn trong một môn thể thao cụ thể. Tuy nhiên: Điều quan trọng là phải biết mối tương quan đó Nói cách khác, hồi quy logistic có thể cho bạn thấy rằng có mối tương quan thuận giữa nhiệt độ ngoài trời và doanh số bán hàng, nhưng điều này không nhất thiết có nghĩa là doanh số bán hàng tăng do nhiệt độ.
Nhược điểm
- Hồi quy logistic không dự đoán được kết quả liên tục. Hãy xem xét một ví dụ để hiểu rõ hơn về hạn chế này. Trong các ứng dụng y tế, hồi quy logistic không thể được sử dụng để dự đoán nhiệt độ của bệnh nhân viêm phổi sẽ tăng cao như thế nào. Điều này là do quy mô đo lường là liên tục (hồi quy logistic chỉ hoạt động khi biến phụ thuộc hoặc biến kết quả là lưỡng phân).
- Hồi quy logistic giả định tính tuyến tính giữa biến dự đoán (phụ thuộc) và biến dự báo (độc lập). Tại sao đây là một hạn chế? Trong thế giới thực, rất khó có khả năng các quan sát được phân tách tuyến tính. Hãy tưởng tượng bạn muốn phân loại cây diên vĩ thành một trong hai họ: sentosa hoặc versicolor. Để phân biệt giữa hai loại, bạn sẽ phân biệt kích thước cánh hoa và kích thước đài hoa. Bạn muốn tạo ra một thuật toán để phân loại cây diên vĩ, nhưng thực sự không có sự phân biệt rõ ràng — một cánh hoa kích thước 2cm có thể đủ tiêu chuẩn cho cây trồng cho cả hai loại màu xanh lá và màu sắc. Vì vậy, trong khi dữ liệu có thể phân tách tuyến tính là giả định cho hồi quy logistic, trên thực tế, nó không phải lúc nào cũng thực sự khả thi.
- Hồi quy logistic có thể không chính xác nếu kích thước mẫu quá nhỏ. Nếu kích thước mẫu ở mức nhỏ, thì mô hình được tạo ra bằng hồi quy logistic dựa trên số lượng quan sát thực tế nhỏ hơn. Điều này có thể dẫn đến trang bị quá nhiều. Trong thống kê, overfitting là một lỗi mô hình hóa xảy ra khi mô hình quá khớp với một bộ dữ liệu hạn chế vì thiếu dữ liệu đào tạo. Hay nói cách khác, không có đủ dữ liệu đầu vào để mô hình tìm ra các mẫu trong đó. Trong trường hợp này, mô hình không thể dự đoán chính xác kết quả của một tập dữ liệu mới hoặc trong tương lai.
1.4. Machine Learning và mô hình dự đoán trong Logistic Regression
Machine Learning (Học máy) sử dụng các khái niệm thống kê để cho phép máy móc (máy tính) “học” mà không cần lập trình rõ ràng. Cách tiếp cận hậu cần phù hợp nhất khi nhiệm vụ mà máy đang học dựa trên hai giá trị hoặc phân loại nhị phân . Sử dụng ví dụ trên, máy tính của bạn có thể sử dụng loại phân tích này để đưa ra các quyết định về việc quảng cáo ưu đãi của bạn và tự thực hiện các hành động. Và, khi cung cấp nhiều dữ liệu hơn, nó có thể học cách thực hiện điều này tốt hơn theo thời gian.
Một số loại mô hình dự đoán sử dụng phân tích logistic:
- Mô hình tuyến tính tổng quát
- Sự lựa chọn rời rạc
- Logit đa thức
- Đăng nhập hỗn hợp
- Probit
- Probit đa thức
- Đăng nhập có thứ tự
2. Mô hình hồi quy Logistic (Logistic Regression Model)
Đầu tiên ta xem giả định của Logistic Regression Model là gì trước nhé!
2.1. Giả định của Logistic Regression Model
- Biến phụ thuộc là biến nhị phân hoặc lưỡng phân — Nó phù hợp với một trong hai loại rõ ràng. Điều này áp dụng cho hồi quy logistic nhị phân, là loại hồi quy logistic mà chúng ta đã thảo luận cho đến nay. Chúng ta sẽ khám phá một số kiểu hồi quy logistic khác trong phần năm.
- Không được có, hoặc rất ít, đa cộng tuyến giữa các biến dự báo — nói cách khác, các biến dự báo (hoặc các biến độc lập) phải độc lập với nhau. Điều này có nghĩa rằng có nên không có một mối tương quan cao giữa các biến độc lập. Trong thống kê, các phép thử nhất định có thể được sử dụng để tính toán mối tương quan giữa các biến dự báo; nếu bạn muốn tìm hiểu thêm về những thứ đó, chỉ cần tìm kiếm “Hệ số tương quan xếp hạng của Spearman” hoặc “Hệ số tương quan Pearson”.
Tham khảo nếu chưa biết Đa cộng tuyến là gì? | Cách tính Hệ số tương quan Pearson
- Các biến độc lập phải có liên quan tuyến tính với tỷ lệ cược log. Nếu bạn không quen thuộc với tỷ lệ cược đăng nhập, chúng tôi đã bao gồm một giải thích ngắn gọn bên dưới.
- Hồi quy logistic yêu cầu kích thước mẫu khá lớn — kích thước mẫu càng lớn, bạn có thể mong đợi kết quả phân tích của mình càng đáng tin cậy (và mạnh mẽ).
2.2. Mô hình xác suất tuyến tính (Linear Probability Model – LPM)
Trước hết chúng ta hãy xét mô hình đơn giản nhưng mô hình này không đúng mặc dù cũng hồi quy trên biến phụ thuộc với 2 giá trị duy nhất 1 và 0. Mô hình xác suất tuyến tính (Linear Probability Model-LPM).
Mô hình này dựa trên giả định rằng xác suất xảy ra sự kiện, Pi là tuyến tính với các biến giải thích:
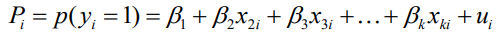
Đây là mô hình hồi quy tuyến tính và có thể ước lượng bằng phương pháp bình phương nhỏ nhất OLS. Tuy việc ước lượng là đơn giản nhưng có 1 số lý do sau đây mà mô hình PLM không phù hợp để mô hình hoá mô hình logistic với biến phụ thuộc là nhị phân.
- Thứ nhất, mô hình LPM giả định rằng xác suất của Pi có mối quan hệ tuyến tính với giá trị của biến giải thích
- Thứ hai, theo tính logit thì giá trị xác suất phải nằm giữa 0 và 1 vì biến phụ thuộc là biến nhị phân. Nhưng không có gì đảm bảo rằng các giá trị xác suất ước lượng từ mô hình LPM sẽ nằm trong các giới hạn này. Điều này là bởi vì OLS không tính đến sự ràng buộc rằng các xác suất ước lượng phải nằm giữa các giới hạn 0 và 1.
- Thứ ba, giả định thông thường rằng hạng nhiễu theo phân phối chuẩn không thể được thỏa mãn khi biến phụ thuộc chỉ nhận các giá trị 0 và 1.
- Cuối cùng, hạng nhiễu trong mô hình LPM có phương sai thay đổi, điều này làm cho các kiểm định ý nghĩa truyền thống không thể tin cậy được
Vì tất cả các lý do trên nên mô hình LPM hay mô hình OLS đều không phải là sự lựa chọn tốt để mô hình hóa các biến nhị phân với các lý do đã liệt kê như trên. Đó là lý do tại sao mô hình logit và probit được sử dụng dể hồi quy các biến phụ thuộc dạng nhị phân (Binary Dependent Variables).
2.2. Mô hình Logit
Mô hình hồi quy Logit có tên này là bởi vì nó đã sử dụng phân phối logit tích lũy (cumulative logistic distribution) đễ chuyển đổi sao cho các giá trị xác suất được ước lượng sẽ tuân theo mô hình chữ S như đã thảo luận trong phần trước.
Giả sử có mô hình biến phụ thuộc là phụ nữ có bầu và không có bầu như sau:
Yi=βX+ui
(Yi = 1 là phụ nữ có bầu và ngược lại với 0)
Khi Yi=1 ta có: Pr(Yi=1 ≥ 0) = Pr[(βX+ui) ≥ 0] = Pr(ui ≥ – βX) hay Pr(ui ≤ – βX)
Từ kết quả có thể thấy Pi phụ thuộc vào phân phối xác suất cụ thể của ui vì xác suất mà một biến ngẫu nhiên nhỏ hơn một giá trị xác định được tính bởi hàm phân phối tích lũy (CDF – cumulative distribution function) của biến đó. Vì vậy, mô hình logit giả định rằng phân phối xác suất của ui theo phân phối xác suất Logistic (Logistic Probability Distribution), theo đó phương trình viết lại như sau:
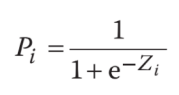
Sau quá trình biến đổi thì phương trình trở thành:
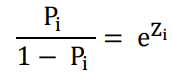
Với e là cơ số mũ tự nhiên tương ứng với phân phối logit vì vậy mô hình Logit sẽ có phương trình hồi quy như sau:
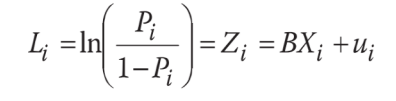
Cứ suy nghĩ đơn giản là hiểu ngay thôi phải không nào, đến đây theo công thức trên thì ta gọi Pi/(1 – Pi) đơn giản là tỷ số odds (odds ratio) ủng hộ việc phụ nữ có bầu – tỷ số của xác suất mà một người phụ nữ mang bầu so với xác suất mà người đó không dính bầu :))).
Lúc này ta gọi log của tỷ số odds là một hàm tuyến tính của các tham số Bs và cũng như các biến Xs. Li được gọi là logit (log của tỷ số odds) và vì thế có tên là mô hình logit (logit model).
Funfact: Mặc dù nhìn Logit như phi tuyến nhưng log của tỷ số odds hay gọi là logt làm cho mô hình logit trở thành tuyến tính trong các tham số.
Tham khảo bài viết Mô hình tuyến tính và phi tuyến tính là gì?
2.3. Mô hình Probit
Trong hồi quy mô hình Probit, hàm phân phối chuẩn chuẩn tích lũy Φ(⋅) được sử dụng để mô hình hóa hàm hồi quy khi biến phụ thuộc là nhị phân, tức là, ta giả sử:
E(Y|X)= P(Y=1|X) = Φ(β0+β1X) = F(BX)
Theo đó: β0+β1X trong ở trên đóng vai trò của một lượng tử z.
Với giả định phân phối chuẩn cho trước như mô hình Logit, thì xác suất để nhỏ hơn hoặc bằng Fi có thể được tính từ hàm phân phối tích lũy chuẩn hóa (CDF – Standard Normal Cumulative Distribution Function) như sau:
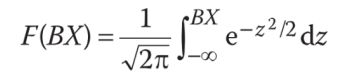
Tổng kết: Mô hình logit sử dụng phân phối xác suất logistic và mô hình probit sử dụng phân phối chuẩn.
2.4. Ước lượng mô hình Logit và Probit
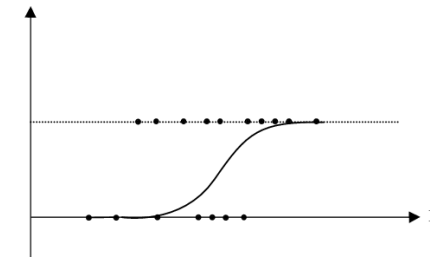
Cả hai mô hình hồi quy logit và probit đều có khả năng khắc phục những nhược điểm là giá trị xác suất ước lượng nhỏ hơn 0 hay lớn hơn 1 của mô hình LPM.
Hai mô hình này sử dụng một hàm số để chuyển đổi một cách có hiệu quả mô hình hồi quy LPM sao cho các giá trị ước lượng chỉ sẽ nằm ở giữa khoảng cách cho phép (0,1).
Trong mô hình LPM thì hạng nhiễu không có phân phối chuẩn; trong mô hình logit và probit thì hạng nhiễu có phân phối lần lượt là logistic và phân phối chuẩn.
Qua đồ thị có thể dẽ dàng nhìn thấy rằng các giá trị ước lượng đã được uốn cong lại theo hình chữ S thay vì là một đường thẳng như trước đây như trong trường hợp
của mô hình LPM.
Vì thế, để ước lượng mô hình logit chúng ta phải dựa vào các phương pháp ước lượng khác thay vì chọn những phương pháp cơ bản dùng để ước lượng như LPM như OLS đã nêu trên. Phương pháp phổ biến nhất với các tính chất thống kê hấp dẫn là phương pháp hợp lý tối đa (ML – maximum likelihood estimation).
Funfact: Không giống mô hình LPM, ảnh hưởng biên (marginal effect) của một biến giải thích trong mô hình Logit và Probit phụ thuộc không chỉ vào hệ số của biến đó mà còn và các giá trị của tất cả các biến giải thích trong mô hình. Trong thực tế, các mô hình logit và probit cho các kết quả tương tự tuỳ lựa chọn của bạn, tuy nhiên đa số nghiên cứu sử dụng mô hình logit.
2.5. Kiểm tra độ phù hợp của mô hình Logit và Probit
Thước đo thông thường về mức độ phù hợp trong mô hình tuyến tính như OLS thường là giá trị R2 không còn ý nghĩa khi biến phụ thuộc nhận các giá trị 1 hoặc 0.
Một thước đo tương tự R2 dùng để kiểm tra độ phù hợp mô hình biến phụ thuộc giới hạn là Pseudo R2 hay còn được gọi là McFadden R2, kí hiệu là R2McF. Giống như R2 thì R2McF nằm giữa 0 và 1. (Sẽ được trình bày trong phần hồi quy bằng phần mềm Stata tại Mục 4)
Một thước đo về mức độ phù hợp khác là count R2 , được định nghĩa như sau:
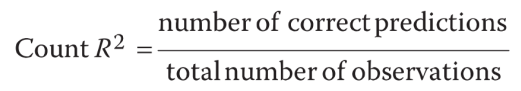
Vì biến phụ thuộc nhận một giá trị 1 hoặc 0, nếu xác suất dự đoán cho một quan sát lớn hơn 0.5 chúng ta phân loại quan sát đó như 1, nhưng nếu nhỏ hơn 0.5, chúng ta phân loại như 0. Sau đó chúng ta đếm số dự đoán đúng và tính count R2 như công thức ở trên
3. Phân loại, Công cụ sử dụng và So sánh hồi quy logistic
3.1. Phân loại
Trên thực tế, có ba kiểu hồi quy logistic khác nhau, bao gồm cả kiểu mà chúng ta hiện đã quen thuộc.
Ba loại hồi quy logistic là:
- Hồi quy logistic nhị phân là kỹ thuật thống kê được sử dụng để dự đoán mối quan hệ giữa biến phụ thuộc (Y) và biến độc lập (X), trong đó biến phụ thuộc có bản chất là nhị phân. Ví dụ, kết quả đầu ra có thể là Thành công / Không thành công, 0/1, Đúng / Sai hoặc Có / Không. Đây là loại hồi quy logistic mà chúng tôi đã tập trung vào trong bài đăng này.
- Hồi quy logistic đa thức được sử dụng khi bạn có một biến phụ thuộc phân loại với hai hoặc nhiều mức không có thứ tự (tức là hai hoặc nhiều kết quả rời rạc). Nó rất giống với hồi quy logistic ngoại trừ việc ở đây bạn có thể có nhiều hơn hai kết quả có thể xảy ra. Ví dụ: hãy tưởng tượng rằng bạn muốn dự đoán loại phương tiện giao thông được sử dụng nhiều nhất vào năm 2030. Loại phương tiện giao thông sẽ là biến phụ thuộc, với các đầu ra có thể có là xe lửa, xe buýt, xe điện và xe đạp (ví dụ).
- Hồi quy logistic thứ tự được sử dụng khi biến phụ thuộc (Y) có thứ tự (tức là thứ tự). Biến phụ thuộc có một thứ tự có ý nghĩa và nhiều hơn hai danh mục hoặc cấp độ. Ví dụ về các biến như vậy có thể là kích thước áo phông (XS / S / M / L / XL), câu trả lời trong cuộc thăm dò ý kiến (Đồng ý / Không đồng ý / Trung lập) hoặc điểm số trong bài kiểm tra (Kém / Trung bình / Tốt).
3.2. Các công cụ sử dụng hồi quy logistic
Hầu hết các phần mềm thống kê có thể thực hiện hồi quy logistic nhị phân. Gồm các phần mềm như dưới đây:
- SPSS
- Stata
- SAS
- R với gói glm trong gói thống kê (sử dụng family = binomial)
- Python
- NCSS, MATLAB, JAVA (JVM), FPGA.
3.3. So sánh hồi quy tuyến tính với hồi quy logistic
Khi nào sử dụng phân tích tuyến tính hoặc phân tích logistic là một truy vấn phổ biến.
Về cơ bản, phân tích hồi quy tuyến tính được áp dụng hiệu quả hơn khi biến phụ thuộc là biến mở hoặc liên tục – chẳng hạn như khoảng cách hoặc nhiệt độ thiên văn.
Sử dụng phương pháp logistic khi biến phụ thuộc bị giới hạn trong một phạm vi giá trị hoặc phân loại – A hoặc B … hoặc A, B, C hoặc D.
Tham khảo: Hồi quy tuyến tính là gì?
4. Logistic Regression trong phần mềm STATA
Tải về bộ dữ liệu VIP “Các nhân tố ảnh hưởng đến quyết định gửi tiền và lượng tiền gửi tiết kiệm vào ngân hàng thương mại” này rồi thực hành thử lun nhé các bạn
[su_button url=”http://destyy.com/eaxR5z” target=”blank” style=”3d” color=”#fefefd” size=”10″ center=”yes” radius=”20″ icon=”icon: download” text_shadow=”0px 0px 0px #000000″ desc=”Tải ngay” download=”Dữ liệu”]DỮ LIỆU MOSL.VN[/su_button]
Hình ảnh dữ liệu trong Excel:
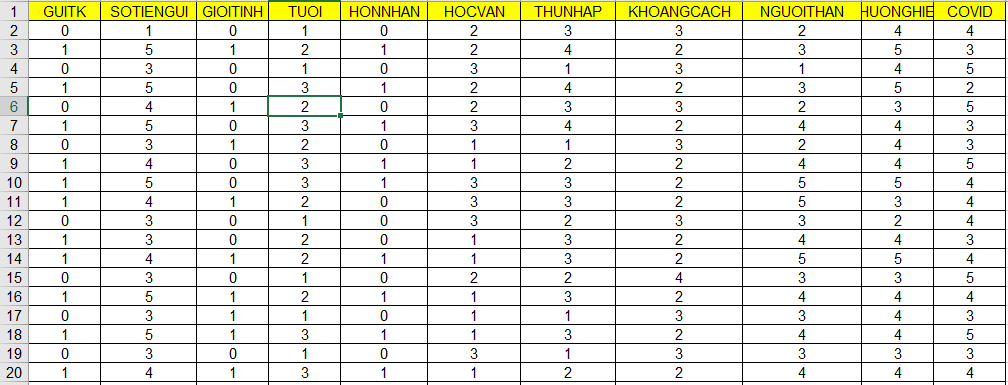
Bộ dữ liệu gồm 200 quan sát cùng 2 biến phụ thuộc GUITK (Có gửi=1; Không gửi=0) và SOTIENGUI (nếu người đó có gửi tiền). 9 biến độc lập gồm các biến nhân khẩu học như GIOITINH (1: Nam; 0: Nữ), TUOI (4 bậc tuổi), HONNHAN (1: Đã kết hôn; 0: chưa), HOCVAN, THUNHAP (4 mức); các biến giải thích gồm KHOANGCACH, NGUOITHAN, THUONGHIEU.
Ai chưa biết sử dụng Stata thì tham khảo bài Hướng dẫn sử dụng Stata nha
4.1. Hồi quy mô hình Probit
Đầu tiên nhập dữ liệu vào phần mềm Stata và dùng lệnh sau để chạy hồi quy mô hình Probit:
probit GUITK GIOITINH TUOI HONNHAN HOCVAN THUNHAP KHOANGCACH NGUOITHAN THUONGHIEUNếu ai chưa biết cách nhập dữ liệu vào Stata thì tham khảo bài này nha
Kết quả như bên dưới:
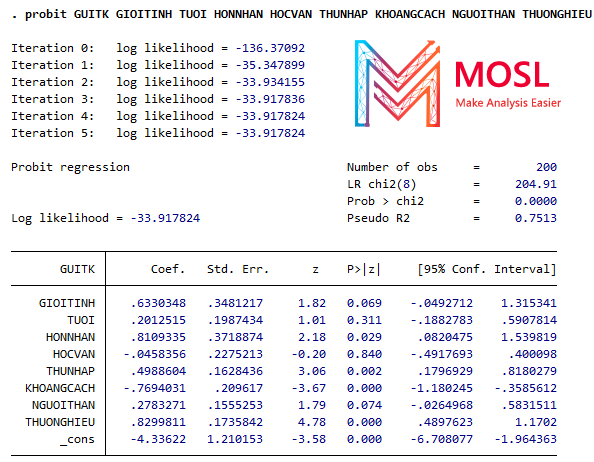
Chú ý: Việc diễn giải kết quả hồi quy đối với mô hình Probi hay cả Logit sẽ có sự khác biệt với mô hình hồi quy tuyến tính. Đọc kỹ cách phân tích bên dưới để áp dụng vô bài tránh sai sót nhé!
Tham khảo thêm Cách đọc kết quả stata hồi quy mô hình OLS
Diễn giải cách đọc kết quả hồi quy Logistic:
- Hệ số hồi quy cho biến GIOITINH = 0.6330 có nghĩa là khi GIOITINH là người nam (Nam=1; Nữ=0 thì hệ số GIOITINH không có nên không xét trường hợp nữ nha), thì LnOdds (GUITK) = ln (Xác suất GUITK = 1/xác suất GUITK=0) – (Đọc là log tỷ số Odds [Log Odd ratio] hoặc trung bình giá trị logit hoặc log xác xuất của người gửi tiết kiệm trên người không gửi tiết kiệm của biến GUITK) sẽ tăng 0,6330 đơn vị.
- Hệ số hồi quy cho biến THUNHAP = 0.4988 có nghĩa là khi THUNHAP tăng lên 1 đồng thì Log tỷ số Odds của GUITK hay log xác xuất của người gửi tiết kiệm trên người không gửi tiết kiệm sẽ tăng 0.4988 đơn vị.
- Tương tự các biến khác, Mosl sẽ làm thêm cho 1 biến tác động ngược chiều có ý nghĩa như là biến KHOANGCACH; Hệ số hồi quy là -0.7694 có nghĩa là khi KHOANGCACH giảm 1 km thì Log tỷ số Odds của GUITK sẽ tăng 0.7694 đơn vị.
- Giá trị Pseudo R2 = 0.7513 có nghĩa rằng các biến độc lập giải thích được 75.13% sự thay đổi trong log (xác xuất của người gửi tiết kiệm trên người không gửi tiết kiệm) của biến phụ thuộc.
- Giá trị Prob>chi2 = 0.0000 giúp bác bỏ H0: Mô hình hồi quy là không phù hợp của kiểm điểm LR test giúp kết luận mô hình Probit hiện tại là phù hợp ok nha.
Lưu ý: Khi phân tích cũng giống như trong mô hình hồi quy tuyến tính nếu biến độc lập không đạt ý nghĩa thống kê hay p-value > 10% thì bạn sẽ không kết luận về biến đó theo kiểu tăng giảm như trên mà đơn giản ghi là kết quả hồi quy của biến A không đạt ý nghĩa thống kê tại bất kỳ mức ý nghĩa nào!
Kiểm tra độ phù hợp của mô hình Probit
Trước khi kiểm tra nhớ cài lệnh fitstat vào Stata bằng code nếu chạy lỗi nha:
ssc install fitstatSau khi hồi quy xong mô hình Probit thực hiện lệnh: fitstat
Kết quả như sau:

Lưu ý: Các giá trị đo lường mức độ phù hợp của mô hình tiêu chuẩn OLS tuyến tính như R2, RSS không còn đúng với mô hình Probit và cả Logit nữa nên phải cần phải có 1 hệ số khác để đo lường phần này.
Ở đây bạn sẽ dựa vào chỉ số McFadden’s R2 (chính là chỉ số Pseudo R2) và giá trị Prob > LR để đánh giá như đánh giá từ kết quả mô hình phía trên cho tiện nhé! Thực ra chạy thêm câu lệnh fitstat này để trình bày cho bài làm màu mè thêm chút thôi :)))
Thế thôi hồi quy mô hình Probit bằng phương pháp ML chỉ đơn giản như vậy.
4.2. Hồi quy mô hình Logit
Cách 1:
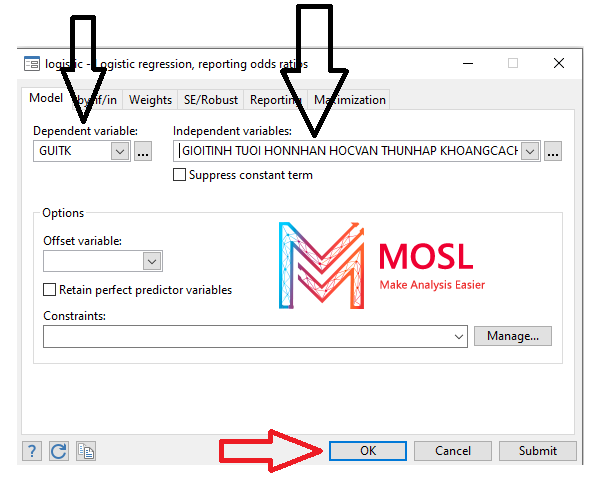
Sử dụng thanh Menu phía bên trên trong phần mềm Stata: Chọn Statistics -> Binary outcomes -> Logistic regression

Kết quả hiện ra bên dưới chỉ cần chọn biến GUITK vào ô biến phụ thuộc và các biến độc lập vào ô biến độc lập, Xong click chọn Ok là có kết quả rồi nhé!
Cách 2:
Dùng code sau:
logit GUITK GIOITINH TUOI HONNHAN HOCVAN THUNHAP KHOANGCACH NGUOITHAN THUONGHIEU
Kết quả tương tự khi thực hiện bằng lệnh như ở cách 1:
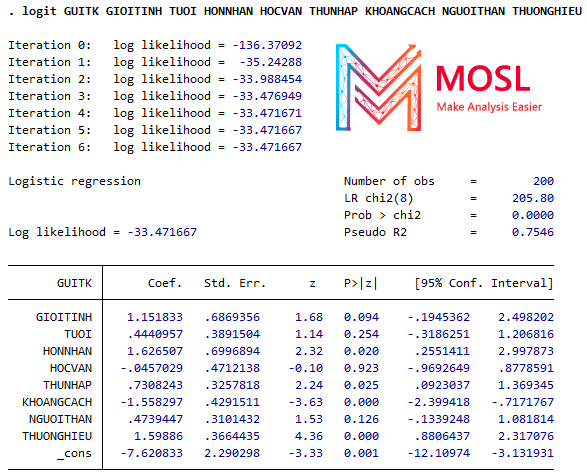
Phân tích tương tự như kết quả từ mô hình Probit phía trên, vì hai ông mô hình Probit & Logit này thực chất là như nhau nha.
Hai mô hình này thì thực hiện chạy Stata vô cùng đơn giản quan trọng bạn phải chú ý đến cách phân tích và số lượng mẫu quan sát phải khá lớn từ 150 mẫu trở lên thì mới cho ra kết quả Stata ok, ngược lại chạy lỗi ráng chịu nha :)))
Tiếp theo tới phân tích xác xuất dự đoán của hiệu ứng từng phần (Average partial effects) và tác động biên (Marginal Effect) đi kèm với 2 mô hình này.
4.3. Hiệu ứng từng phần (Average partial effects) và tác động biên (Marginal Effect)
Hai mô hình là tương tự nhau ở đây MOSL lấy mô hình Logit làm ví dụ cho đa dạng hee
Hiệu ứng từng phần (Average Partial Effects)
Hiệu ứng từng phần tính toán các hiệu ứng cận biên trung bình và sai số tiêu chuẩn cho các hiệu ứng biên bằng phương pháp delta. Thay vì tính toán các hiệu ứng biên tại các giá trị của các biến hoặc tại các giá trị do người dùng chỉ định (Tác động biên – Marginal Effect), thì Average Partial Effects tính toán giá trị trung bình của các thay đổi từng phần và rời rạc qua các quan sát.
Sau khi hồi quy mô hình logit bằng lệnh:
logit GUITK GIOITINH TUOI HONNHAN HOCVAN THUNHAP KHOANGCACH NGUOITHAN THUONGHIEU ở trên rồi thì tiếp tục sử dụng lệnh: margeff (Nếu chưa cài thì gõ ssc install margeff để cài rồi chạy nha)
Kết quả như bên dưới
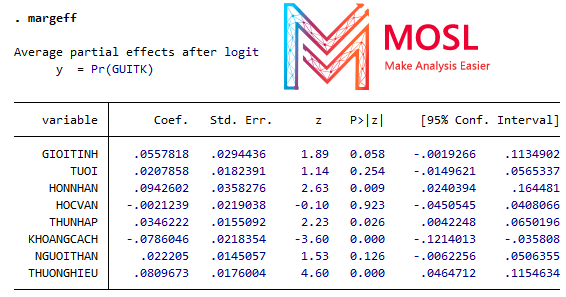
Đọc kết quả thì đề cập đến các biến có trung bình ảnh hưởng từng phần lên biến phụ thuộc thôi nha.
Tác động biên (Marginal Effect)
Tác động biên tính toán các hiệu ứng biên tại các giá trị của các biến hoặc tại các giá trị do người dùng chỉ định
Ví dụ 1. Tính toán hiệu ứng biên tại giá trị trung bình của các biến Code sau: margins, atmean (Nếu không muốn tính trung bình thì đơn giản nhập margins thôi là được) – Nếu chưa cài thì gõ ssc install margins để cài rồi chạy nha.
Kết quả:
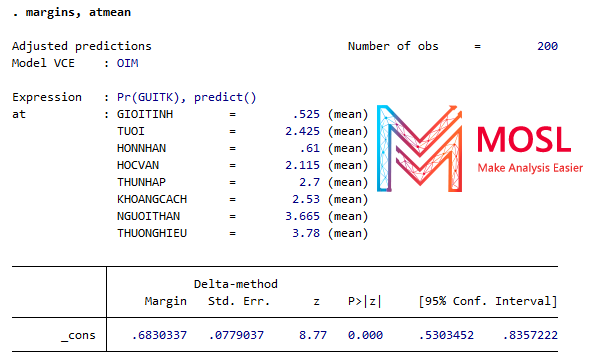
Giải thích: Xác suất của GUITK = 1 (tức có gửi tiết kiệm) là 68% khi tất cả các yếu tố dự đoán là các biến độc lập tại giá trị trung bình của chúng.
Ví dụ 2. Thêm thắt 1 chút tính giá trị biên khi GIƠITINH=0 chẳng hạn, code và kết quả bên dưới:
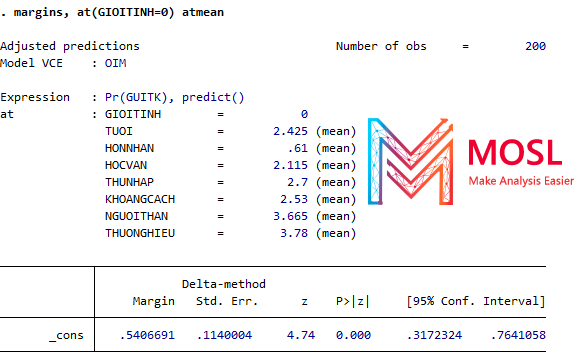
Giải thích: Xác suất của GUITK = 1 (tức có gửi tiết kiệm) là 54% khi GIOITINH = 0 (tức là nữ) cùng với tất cả các yếu tố dự đoán là các biến độc lập còn lại tại giá trị trung bình của chúng.
Ví dụ 3. Lần này tính tác động biên tại 3 biến GIOITINH TUOI và THUNHAP cùng 1 lúc thử như nào :))) . Kết quả và code như trong hình.
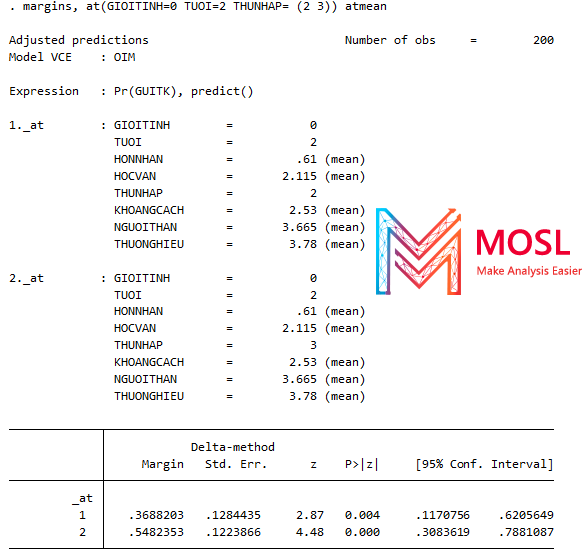
Giải thích:
- Xác suất của GUITK = 1 (tức có gửi tiết kiệm) là 36% khi GIOITINH = 0 (tức là nữ); TUOI=2 (Khoảng trên 22 tuổi đến 30) cùng THUNHAP=2 (Từ 10 -15tr/ tháng) cùng với tất cả các yếu tố dự đoán là các biến độc lập còn lại tại giá trị trung bình của chúng.
- Xác suất của GUITK = 1 (tức có gửi tiết kiệm) là 54% khi GIOITINH = 0 (tức là nữ); TUOI=2 (Khoảng trên 22 tuổi đến 30) cùng THUNHAP=3 (Từ 15-20tr/tháng) cùng với tất cả các yếu tố dự đoán là các biến độc lập còn lại tại giá trị trung bình của chúng.
Ví dụ 4. Lần này thêm lệnh i.KHOANGCACH vào biến KHOANGCACH của mô hình logit giúp tính các giá trị biến giả bên trong xem sao. Code và kết quả như hình dưới:
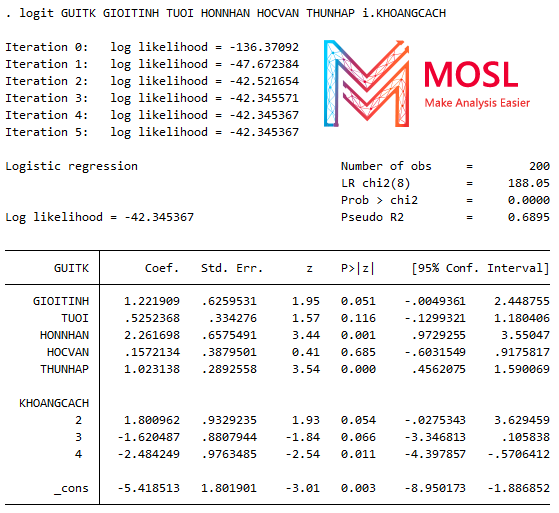
Sau khi hồi quy mô hình logit xong thì tính tác động biên của KHOANGCACH thử nhé!
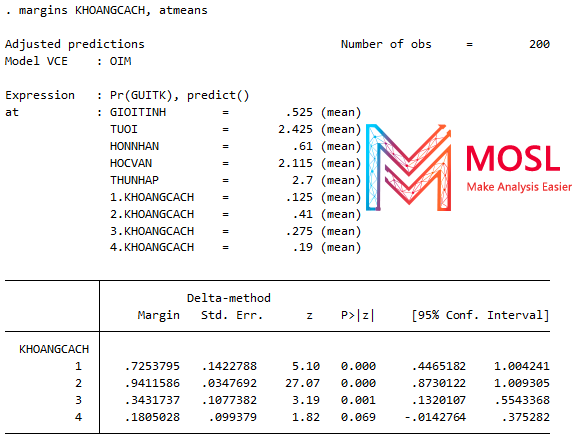
Giải thích: Giữ tất cả các biến ở giá trị trung bình (atmean). Xác suất của GUITK = 1 là:
• 72% trong số những người có KHOANGCACH=1 (từ 1-2km);
• 94% trong số những người có KHOANGCACH=2 (từ 3-4km)
• 34% trong số những người có KHOANGCACH=3 (từ 5-6km)
• 18% trong số những người có KHOANGCACH=4 (Trên 7km)
Tổng kết 5. Sau khi chạy tác động biên bên trên xong có thể vẽ luôn cái biểu đồ tác động biên cho nó cool ngầy nha quý zị
Sau khi tính tác động trong ví dụ 4 bạn sẽ dùng code sau: marginsplot để vẽ biểu đồ tác động biên
Kết quả như sau:
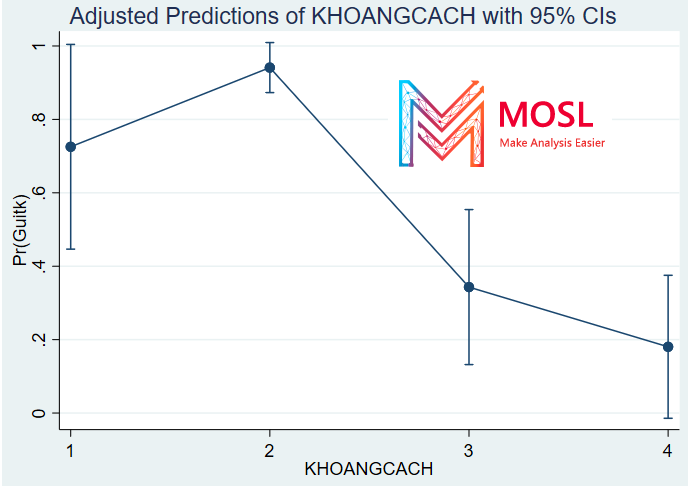
Các phần chạy phía trên MOSL đã cung cấp cho các bạn đa dạng cách chạy tác động biên (marginal efect) trong 2 mô hình probit và logit. Cần câu đã có thêm mắm thêm muối biến tấu như nào là ở bạn, nếu khó khăn hãy gõ: help marginal trong stata
5. Ứng dụng của hồi quy logistic
Đánh giá rủi ro tín dụng
Sử dụng hồi quy logistic nhị phân để đánh giá rủi ro tín dụng. Nếu bạn là một nhân viên cho vay của một ngân hàng, thì bạn muốn có thể xác định các đặc điểm chỉ ra những người có khả năng vỡ nợ và sử dụng các đặc điểm đó để xác định rủi ro tín dụng tốt và xấu.
- Giả sử thông tin về 850 khách hàng trong quá khứ và khách hàng tiềm năng được chứa trong 1 file dữ liệu. 700 trường hợp đầu tiên là những khách hàng đã được cho vay trước đó. Sử dụng một mẫu ngẫu nhiên trong số 700 khách hàng này để tạo mô hình hồi quy logistic, đặt các khách hàng còn lại sang một bên để xác nhận phân tích. Sau đó, sử dụng mô hình để phân loại 150 khách hàng tiềm năng là rủi ro tín dụng tốt hay xấu.
- Tương tự như vậy, một công ty mỹ phẩm có thể muốn xác định xem một khách hàng nhất định có khả năng phản hồi tích cực đối với ưu đãi khuyến mại 2 tặng 1 trên dòng sản phẩm chăm sóc da của họ hay không? Trong trường hợp đó, họ có thể sử dụng hồi quy logistic để đưa ra mô hình dự đoán liệu khách hàng sẽ là “người phản hồi” hay “người không phản hồi”. Dựa trên những thông tin chi tiết này, họ sẽ có ý tưởng tốt hơn về nơi cần tập trung các nỗ lực tiếp thị của mình.
Xác định hồ sơ người tiêu dùng hàng hóa đóng gói
Sử dụng hồi quy logistic đa thức cho hồ sơ người tiêu dùng hàng hóa đóng gói
- Là một phần trong nỗ lực cải thiện hoạt động tiếp thị các lựa chọn bữa sáng của mình, một công ty Hàng tiêu dùng đóng gói thăm dò ý kiến của 880 người, ghi nhận tuổi tác, giới tính, tình trạng hôn nhân và liệu họ có lối sống năng động hay không (dựa trên việc họ có tập thể dục ít nhất hai lần hay không. một tuần). Sau đó, mỗi người tham gia được nếm 3 món ăn sáng và được hỏi họ thích món nào nhất.
- Và các bạn có thể đơn giản sử dụng hồi quy logistic đa thức để xác định hồ sơ tiếp thị cho mỗi tùy chọn bữa sáng.
6. Tống kết
Vậy là bạn đã có nó: Giới thiệu đầy đủ về hồi quy logistic. Dưới đây là một số điểm cần tóm tắt để tóm tắt những gì chúng tôi đã đề cập:
- Hồi quy logistic được sử dụng cho các bài toán phân loại khi đầu ra hoặc biến phụ thuộc là phân đôi hoặc phân loại.
- Có một số giả định chính cần được ghi nhớ khi thực hiện hồi quy logistic (xem phần ba).
- Có nhiều loại phân tích hồi quy và các loại hồi quy logistic khác nhau. Điều quan trọng là chọn đúng mô hình hồi quy dựa trên các biến phụ thuộc và độc lập của dữ liệu của bạn.
Hy vọng rằng bài đăng này hữu ích, MOSL xin chúc các bạn học tập và làm việc hiệu quả!
Xem thêm: Dịch vụ Stata của Mosl.vn
[su_box title=”Liên hệ: ” style=”glass” box_color=” #51d7bb “] Hotline: 0707.33.9698 hoặc Mail: sales@mosl.vn | Fanpage: Mentor Of Số Liệu – Mosl.vn . ĐIỀN THÔNG TIN ĐỂ NHẬN TƯ VẤN ngay Tại đây [/su_box]








