Chưa có sản phẩm trong giỏ hàng!
-
04 Tháng 01, 2022
-
1706 views
Mô hình Tobit – Hướng dẫn CỰC chi tiết trong Stata
Mô hình tobit hay còn được gọi là mô hình hồi quy bị kiểm duyệt (censored regression model), mô hình hình thành để ước tính mối quan hệ tuyến tính giữa các biến khi biến phụ thuộc có kiểm duyệt bên trái (left-censored) hoặc bên phải (right-censored).
Trong các mô hình logit và probit MOSL đã thảo luận trước đây, biến phụ thuộc được giả định có các giá trị 0 và 1 (biến nhị phân – binary variable hay là biến phụ thuộc bị giới hạn). Như đã lưu ý, mô hình logit sử dụng phân phối xác suất logistic và mô hình probit sử dụng phân phối chuẩn. Ở đây thì mô hình Tobit cũng là một trong những mô hình có biến phụ thuộc bị giới hạn (limited dependent variable regression models).
Việc kiểm duyệt bên phải diễn ra khi các trường hợp biến phụ thuộc có giá trị bằng hoặc cao hơn ngưỡng nào đó, nhưng đều lấy giá trị của ngưỡng đó (cho dù giá trị thực có thể bằng ngưỡng, nhưng nó cũng có thể cao hơn). Trong trường hợp kiểm duyệt từ bên trái, giá trị của biến phụ thuộc cũng được gán bằng giá trị ngưỡng thấp nhất (cho dù biến phụ thuộc đó có thể có giá trị thấp hơn nữa).
Trong bài viết này Mosl còn bàn luận thêm về mô hình hồi quy bị cắt bỏ (truncated regression model) và so sánh nó với mô hình hồi quy bị kiểm duyệt (censored regression model) cực chi tiết và không ở đâu ngoài ở MOSL có trình bày vấn đề này. Vì kiến thức là để sẽ chia còn bạn nào không làm được thì ib Mosl hỗ trợ tận tình ạ.
Ai chưa biết sử dụng Stata thì tham khảo bài Hướng dẫn sử dụng Stata nha
1. Mô hình Tobit
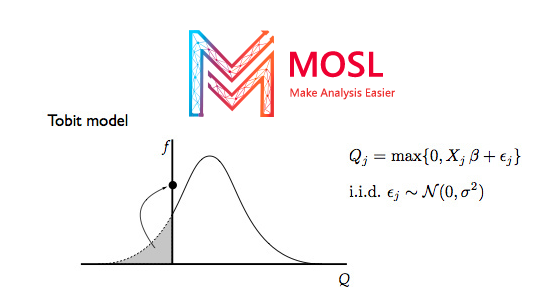
[su_quote cite=”mosl.vn” url=””] Mô hình tobit còn được gọi là mô hình hồi quy bị kiểm duyệt (censored regression model), mô hình hình thành để ước tính mối quan hệ tuyến tính giữa các biến khi biến phụ thuộc có kiểm duyệt bên trái (left-censored) [nghĩa là nó không thể nhận một giá trị dưới một ngưỡng nhất định, điển hình là ngưỡng bằng 0] hoặc bên phải (right-censored) [nghĩa là không nhận một ngưỡng nhất định]. [/su_quote]
[su_quote cite=”https://en.wikipedia.org/wiki/Tobit_model” url=”mosl.vn”] Trong thống kê, mô hình tobit và bất kỳ mô hình hồi quy nào trong đó phạm vi quan sát của biến phụ thuộc được kiểm duyệt theo một cách nào đó theo Arthur Goldberger liên quan đến James Tobin (1958). Bởi vì phương pháp của Tobin có thể dễ dàng mở rộng để xử lý các mẫu bị cắt ngắn và không được chọn ngẫu nhiên khác, một số tác giả áp dụng một định nghĩa rộng hơn về mô hình tobit bao gồm những trường hợp này. [/su_quote]
Ví dụ:
- Trong bài này Mosl làm về quyết định gửi tiền tiết kiệm cùng với số tiền gửi tiết kiệm của khách hàng. Theo đó khách hàng nào mà quyết định sẽ gửi tiết kiệm thì khách hàng đó đương nhiên ta biết được lượng tiền họ gửi; Ngược lại nếu họ không có quyết định gửi thì số tiền gửi của ta không dự đoán được và nó trở thành giá trị 0 – và đây chính là giá trị bị ẩn hay ta xem số tiền gửi sẽ là biến phụ thuộc bị kiểm duyệt.
- Ví dụ đơn giản khác: Khi bạn thu thập dữ liệu về thu nhập của khách hàng, đương nhiên sẽ có người trả lời đúng hoặc không trả lời thì những người không trả lời đấy chính là dữ liệu bị ẩn mà bạn không tìm được. Vậy tồn tại trong biến Thu nhập là 2 trường phái, một là thu được dữ liệu và 2 là không thu được dữ liệu (đa phần đều cho =0 – Không tính đến TH bạn fake thành số cụ thể thì nó không bị ẩn nên Mosl không nói vì nếu vậy dùng MH Logit&Probit là làm được rồi).
Có nhiều biến thể của mô hình Tobit, nhưng ở đây MOSL xét mô hình đơn giản nhất, được gọi là mô hình Tobit chuẩn (standard Tobit model). Mosl sẽ tiếp tục với dữ liệu “Các yếu tố ảnh hưởng đến quyết định gửi tiết kiệm tại ngân hàng thương mại”. Tải về bằng cách bấm vào liên kết dưới đây để cùng nhau thực hành nào:
[su_button url=”http://destyy.com/eaxR5z” target=”blank” style=”3d” color=”#fefefd” size=”10″ center=”yes” radius=”20″ icon=”icon: download” text_shadow=”0px 0px 0px #000000″ desc=”Tải ngay” download=”Dữ liệu”]DỮ LIỆU MOSL.VN[/su_button]
Để biết các quan sát kiểm duyệt được xử lý như thế nào, Mosl sử dụng mô hình mẫu sau:
Yi = B1GIOITINH + B2TUOI + B3HONNHAN + B4HOCVAN + B5THUNHAP + B6KHOANGCACH + B7NGUOITHAN + B8THUONGHIEU + ui
(yi = 1 khi yi > 0 và yi = 0 khi yi ≤ 0)
Trong đó: Hai biến phụ thuộc GUITK (Có gửi tiền tiết kiệm=1; Không gửi TK=0) và SOTIENGUI (nếu người đó có gửi tiền TK). 9 biến độc lập là các biến giải thích gồm các biến nhân khẩu học như GIOITINH (1: Nam; 0: Nữ), TUOI (4 bậc tuổi), HONNHAN (1: Đã kết hôn; 0: chưa), HOCVAN, THUNHAP (4 mức); KHOANGCACH, NGUOITHAN, THUONGHIEU.
Biến Yi được gọi là một biến tiềm ẩn (latent variable). Trong mô hình probit, Yi = 1 nếu Yi lớn hơn 0, và nó bằng 0 nếu biến tiềm ẩm bằng 0.
Trong mô hình Tobit, Yi có thể nhận bất kỳ các giá trị nào miễn là biến tiềm ẩn lớn hơn 0. Đó là lý do tại sao mô hình Tobit cũng được gọi là probit của Tobin.
Xem ngay đừng bỏ lỡ bài viết Mô hình Logit và Probit cực chi tiết nhé!
1.1. Ước lượng ML
Nếu tham số mối quan hệ beta được ước tính bằng cách hồi quy những gì quan sát được trên, kết quả ước lượng hồi quy bình phương nhỏ nhất (Mô hình OLS) thông thường không nhất quán . Nó sẽ mang lại một ước tính chệch hướng xuống của hệ số góc và ước tính chệch hướng lên của hệ số chặn. Takeshi Amemiya (1973) đã chứng minh rằng công cụ ước tính khả năng xảy ra tối đa do Tobin đề xuất cho mô hình này là nhất quán
Để ước lượng một mô hình mà ở đó một số quan sát về biến phụ thuộc bị kiểm duyệt (bởi vì chúng không được quan sát), mô hình Tobit sử dụng phương pháp hợp lý tối đa (ML), mà chúng ta đã gặp trong nhiều trường hợp
1.2. Hồi quy mô hình Tobit trong Stata
Để tạo mô hình tobit trong Stata, hãy liệt kê biến kết quả theo sau là các yếu tố dự đoán và sau đó chỉ định giới hạn dưới (lower limit) và / hoặc giới hạn trên (upper limit) của biến kết quả. Giới hạn dưới được chỉ định trong ngoặc đơn sau ll và giới hạn trên được chỉ định trong ngoặc đơn sau ul. Mô hình tobit có thể được sử dụng để dự đoán một kết quả được kiểm duyệt từ phía trên, từ phía dưới hoặc cả hai (Có người đọc bên trái hay bên phải cũng đúng nha).
Ở mô hình Logit và Probit trong Logistic Regression trước chúng ta đã sử dụng biến phụ thuộc là GUITK (Đánh giá xem quyết định gửi tiền tiết kiệm là có hay không) thì giờ với mô hình Tobit ta sẽ sử dụng biến SOTIENGUI (Lượng tiền mà khách NẾU HỌ CÓ GỬI TIỀN) để diễn đạt rõ mô hình này. Với bộ dữ liệu đã nêu trên ta cùng xem tổng quan về các biến trong mô hình trước nhé!
Lệnh chạy:
sum SOTIENGUI GIOITINH TUOI HONNHAN HOCVAN THUNHAP KHOANGCACH NGUOITHAN THUONGHIEU
Kết quả:
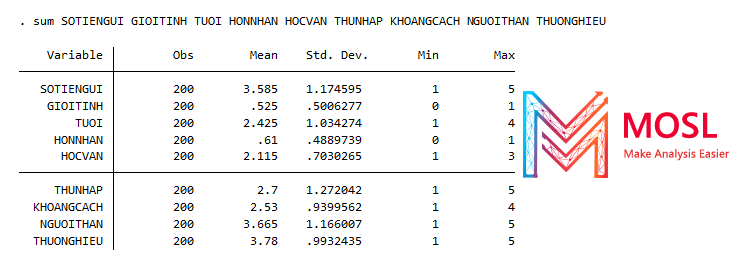
Tiếp đến ta kiểm tra thử biến SOTIENGUI có phải là biến phụ thuộc bị kiểm duyệt mà ta mong đợi không bằng cách vẽ đồ thị Histogram cho nó xem sao nhé!
Lệnh:
histogram SOTIENGUI,normal bin(10)Kết quả:
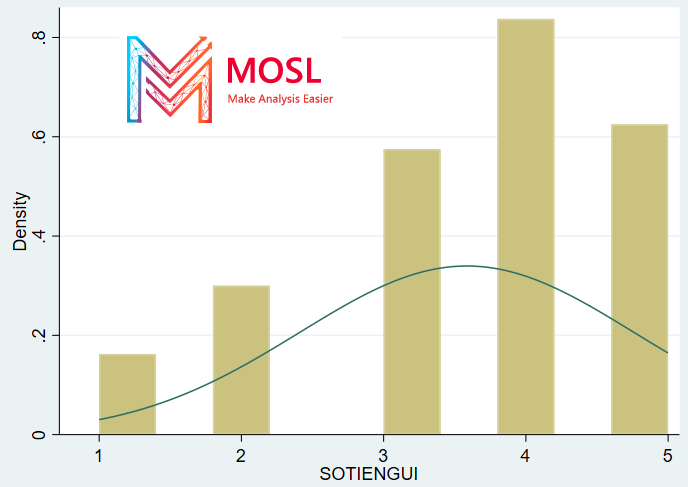
Chú ý SOTIENGUI được mã hoá từ 1 đến 5 với các mức số tiền gửi theo 5 bậc chia từ 10tr đến 100tr trở lên.
Nhìn vào biểu đồ Histogram ở trên cho thấy sự phân bố của SOTIENGUI, bạn có thể thấy sự kiểm duyệt trong dữ liệu, nghĩa là có nhiều trường hợp có điểm số từ trước Mức 1 và sau Mức 5 hơn bạn mong đợi khi nhìn vào phần còn lại của phân phối chuẩn của biến. Vậy đơn giản kết luận rằng biến SOTIENGUI chính là biến phụ thuộc bị kiểm duyệt mà chúng ta đang tìm.
Bây giờ cùng vào thẳng hồi quy mô hình Tobit trong Stata xem như thế nào hee. Vì mức dưới là 1 và mức trên là 5 thì mình sẽ dùng code cho giới hạn dưới (lower limit) là 1 và giới hạn trên (upper limit) là 5 nhé!
Lệnh:
tobit SOTIENGUI GIOITINH TUOI HONNHAN HOCVAN THUNHAP KHOANGCACH NGUOITHAN THUONGHIEU, ll(1) ul(5)Kết quả:
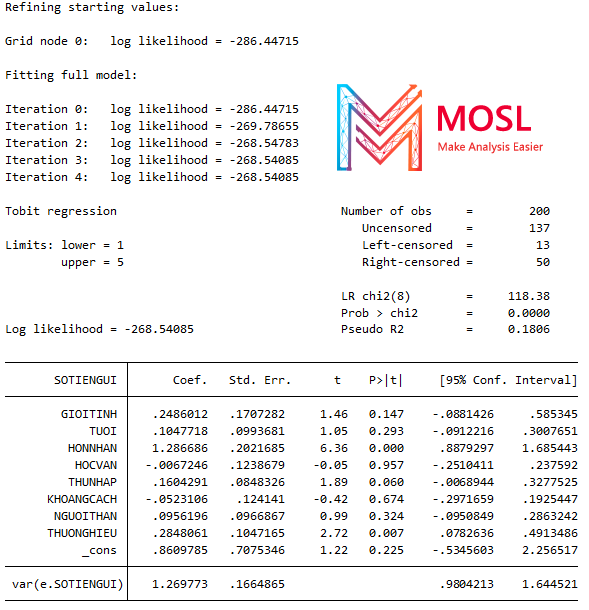
Kết quả trả về với giá trị lower limit = 1 và upper limit = 5. Ta cùng đi vào phần giải thích kết quả để hiểu rõ cách phân tích nào.
1.2. Giải thích Tobit
- Log likelihood – Đây là hệ số Log likelihood của mô hình Tobit. Nó được sử dụng trong kiểm tra Tỷ lệ hợp lí Likelihood Chi-Square về giả thuyết liệu tất cả các hệ số hồi quy của các yếu tố dự đoán trong mô hình có đồng thời bằng 0 hay không (Hay còn gọi là kiểm tra độ phù hợp của mô hình).
- Number of obs – Đây là số lượng quan sát trong tập dữ liệu mà tất cả các biến phản hồi và dự đoán đều không bị thiếu.
- LR chi2(8) – Đây là kiểm định Chi-Square tỷ lệ khả năng xảy ra (LR) mà ít nhất một trong các hệ số hồi quy của người dự đoán không bằng 0. Con số trong ngoặc đơn cho biết bậc tự do của phân phối Chi-Square được sử dụng để kiểm tra thống kê Chi-Square của LR và được xác định bởi số lượng các yếu tố dự đoán trong mô hình Tobit.
- Prob> chi2 – Đây là xác suất nhận được một thống kê kiểm định LR bằng hoặc cao hơn so với thống kê được quan sát trong giả thuyết H0: là tất cả các hệ số hồi quy đồng thời bằng không.
- Pseudo R2 – Đây là R bình phương của McFadden sử dụng trong Hồi quy Tobit, Tobit hay mô hình Logit và Probit đều không có giá trị tương đương với bình phương R được tìm thấy trong hồi quy OLS. Pseudo R2= 0.1806 tức các biến độc lập dự đoán giải thích được 18.06% sự thay đổi trong biến phụ thuộc tiềm ẩn (Nơi mà số tiền gửi không có dữ liệu vì khách hàng họ đâu có quyết định gửi tiền mà sao ta có được số liệu lượng tiền họ gửi phải không) :)))
- Std. Err. – Đây là những sai số tiêu chuẩn của các hệ số hồi quy riêng lẻ. Chúng được sử dụng trong cả việc tính toán thống kê kiểm định t, chỉ số trên i và khoảng tin cậy của hệ số hồi quy, chỉ số trên k.
- t – Thống kê kiểm định t là tỷ số của Coef. đến Std. Err. của công cụ dự đoán tương ứng. Giá trị t được sử dụng để kiểm tra giả thuyết thay thế hai mặt là Coef. không bằng không.
- Trong bảng, chúng ta thấy các hệ số, sai số chuẩn của chúng, thống kê t, các giá trị p-value và khoảng tin cậy 95% của các hệ số.
Tham khảo bài viết Cách đọc kết quả hồi quy mô hình trong Stata nha!
Hệ số hồi quy Tobit được giải thích theo cách tương tự với hệ số hồi quy OLS; tuy nhiên, tác động tuyến tính là trên biến tiềm ẩn Yi (Biến Yi trong trường hợp mà khách hàng không có quyết định gửi tiền thì đương nhiên lượng tiền gửi của họ tức (SOTIENGUI) là không có mà không có thì bạn sẽ cho là 0 – mà đã là 0 thì đó chính là biến tiềm ẩn chưa được kiểm duyệt) – (Bên cạnh còn có thêm 1 tác động nữa sẽ bàn ở bên dưới phần giải thích)
Nhớ là HSHQuy chỉ quan sát biến tiềm ẩn của SOTIENGUI không phải là biến SOTIENGUI mà có thể quan sát được (tức các khách hàng có quyết định gửi tiền thì đương nhiên chúng ta có được thông tin về số tiền gửi của họ vậy thì đơn giản dùng mô hình Logit để làm chứ phải dùng ông Tobit để làm gì ha :))) Sâu xa là vì không quan sát được thế nên mới sử dụng ông Tobit này. – (Tham khảo thêm McDonald và Moffitt (1980) để tìm hiểu kỹ hơn nhé!
Đọc hệ số kết quả hồi quy cho các biến có ý nghĩa tức đạt ý nghĩa thống kê với giá trị P-value thoả mãn < hơn 10% gồm:
- HONNHAN đạt ý nghĩa thống kê tại mức ý nghĩa 1% (Vì p-value=0.000) có nghĩa là khi HONNHAN là 1 tức đã kết hôn thì giá trị dự đoán của SOTIENGUI tăng lên 1.2866 đơn vị trong điều kiện các yếu tố khác không đổi.
- THUNHAP đạt ý nghĩa thống kê tại mức ý nghĩa 10% (Vì p-value=0.060) có nghĩa là khi THUNHAP tăng lên 1 đơn vị thì giá trị dự đoán của SOTIENGUI ( tức khi mà khách hàng đó thay đổi quyết định từ không gửi sang gửi tiết kiệm) thì số tiền gửi họ gửi dự đoán tăng lên 0.1604 đơn vị trong điều kiện các yếu tố khác không đổi.
- THƯƠNGHIEU đạt ý nghĩa thống kê tại mức ý nghĩa 1% (vì p-value= 0.007) có nghĩa là khi thương hiệu của ngân hàng tăng lên 1 đơn vị thì giá trị dự đoán về số tiền gửi (tức khi mà khách hàng thay đổi quyết định từ không gửi sang gửi tiền) sẽ tăng lên 0.2848 đơn vị trong điều kiện các yếu tố khác không đổi.
- Các biến còn lại trong mô hình không đạt ý nghĩa thống kê nên MOSL không giải thích tác động mà chỉ kết luận rằng các biến đó không đạt ý nghĩa thống kê trong mô hình Tobit vì p-value > 10%.
Chú ý: Có 1 cái khác giữa OLS và Tobit 1 chút là bạn không thể giải thích hệ số của Tobit của một biến giải thích như tác động biên của biến giải thích đó lên giá trị trung bình của biến phụ thuộc được quan sát. Điều này là bởi vì trong các mô hình Tobit, thì một sự thay đổi đơn vị trong giá trị của một biến giải thích có hai ảnh hưởng: (1) là ảnh hưởng lên giá trị trung bình của biến phụ thuộc quan sát được không ẩn, và (2) là ảnh hưởng lên xác suất mà Yi (biến tiếm ẩn) được quan sát.
Thế nên phần giải thích đọc kết quả phía trên chỉ mới là giải thích về xác xuất mà biến tiềm ẩn được quan sát và chưa đề cập thêm ảnh hưởng biên lên giá trị trung bình của biến phụ thuộc cả ẩn và không ẩn. Tới đây đơn giản thao tác thêm về ảnh hưởng biên lên mô hình Tobit là xong cả hai cách tác động luôn bằng câu lệnh:
margin, atmean (ảnh hưởng biên lên giá trị trung bình nên phải dùng thêm atmean để làm ha)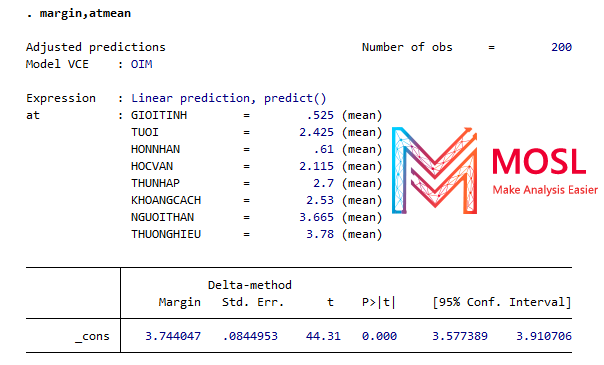
Giải thích: Lượng tiền gửi hay SOTIENGUI dự đoán sẽ là 3.7440 (trong khoảng từ 50-70tr) và đạt ý nghĩa thống kê khi tất cả các yếu tố dự đoán là các biến độc lập tại giá trị trung bình của chúng.
Các biến thể màu mè khác trong lệnh margin đã được bàn trong bài viết về Logistic Regression nên Mosl không trình bày nữa nha.
Cuối cùng, có thể vẽ cái biểu đồ cho tác động biên này bằng lệnh: marginsplot
Kết quả như sau:
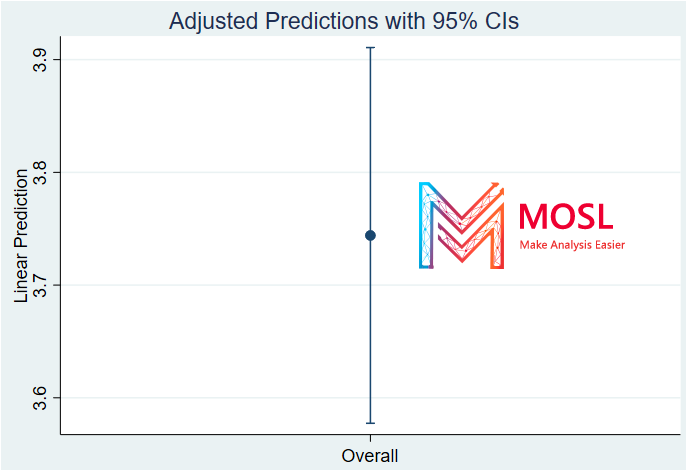
Cái plot này cũng ra kết quả tương tự khi chạy tác động biên (Marginal Effect) nhất quán nhỉ :)))
1.3. Hạn chế của mô hình Tobit
Mô hình Tobit có ít nhất hai nhược điểm chính mà chúng ta cần nắm rõ:
- Trước hết, kết quả mô hình Tobit bị ảnh hưởng tiêu cực nhiều hơn từ hiện tượng phương sai thay đổi (heteroscedasticity ) và phần dư không có phân phối chuẩn (non-normality) so với mô hình hồi quy thông thường (standard regression models) và do vậy các ước lượng sẽ bị “biased” và “inconsistent”.
- Thứ hai là mô hình Tobit yêu cầu rằng biến phụ thuộc có thể có các giá trị gần tới mức giới hạn (limit).
Ví dụ: Khi mua cổ phiếu của công ty IPO (lên sàn chứng khoán) thì vì nhu cầu mua cổ phiếu có thể là 250 cổ phần.
- Tuy nhiên sẽ là không phù hợp cho việc lựa chọn mô hình Tobit trong những tình huống mà biến phụ thuộc là số lượng cổ phần phát hành bởi mỗi công ty trong một tháng nào đó.
- Vì hầu hết các công ty, số lượng phát hành có thể chính xác là 0, nhưng với những công ty có phát hành cổ phần mới thì số lượng cổ phần có thể là rất lớn và do đó không thể có những công ty mà lượng cổ phần phát hành mới chỉ là 1, 3 hay 5 cổ phần.
- Trong trường hợp này sử dụng phương cách tiếp cận khác là cần thiết
2. Các biến thể của mô hình Tobit và Ứng dụng
Các biến thể của mô hình tobit có thể được tạo ra bằng cách thay đổi địa điểm và thời điểm kiểm duyệt xảy ra. Amemiya (1985 , trang 384) phân loại các biến thể này thành năm loại (tobit loại I – loại tobit V), trong đó loại tobit I là viết tắt của mô hình đầu tiên được mô tả ở trên. Schnedler (2005) đưa ra một công thức chung để có được các công cụ ước tính khả năng nhất quán cho các biến thể này và các biến thể khác của mô hình tobit.
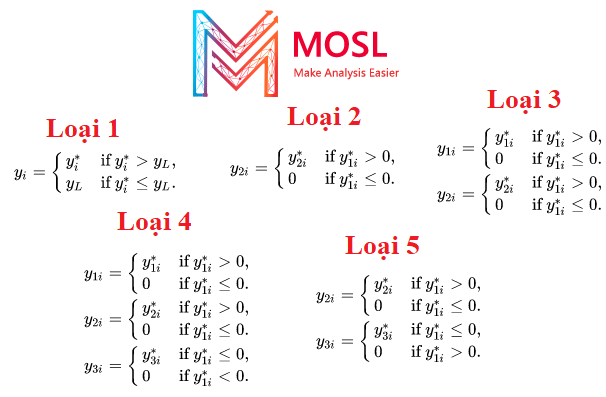
Các biến thể của mô hình Tobit gồm:
Loại I
Mô hình tobit là một trường hợp đặc biệt của mô hình hồi quy có kiểm duyệt , vì biến tiềm ẩn 


Loại II
Trong tobit loại I, biến tiềm ẩn hấp thụ cả quá trình tham gia và kết quả quan tâm. Tobit loại II cho phép quá trình tham gia (lựa chọn) và kết quả quan tâm là độc lập, có điều kiện dựa trên dữ liệu quan sát được.
Mô hình lựa chọn Heckman rơi vào tobit Loại II, mà đôi khi được gọi là Heckit theo tên James Heckman.
Loại III
Loại III giới thiệu một biến phụ thuộc quan sát thứ hai. Heckman cũng rơi vào loại này
Loại IV
Loại IV giới thiệu biến phụ thuộc quan sát thứ ba và biến tiềm ẩn thứ ba.
Loại V
Tương tự như loại II, trong loại V chỉ có dấu hiệu của
Phiên bản không có tham số
Nếu biến tiềm ẩn cơ bản 

Ứng dụng của mô hình Tobit
Ví dụ, các mô hình Tobit đã được áp dụng để ước tính các yếu tố ảnh hưởng đến việc nhận trợ cấp, bao gồm cả các khoản chuyển tài chính được phân phối cho các chính phủ cấp dưới quốc gia, những người có thể nộp đơn xin các khoản trợ cấp này. Trong những trường hợp này, những người nhận tài trợ không thể nhận được số tiền âm, và dữ liệu do đó bị kiểm duyệt.
Ví dụ, Dahlberg và Johansson (2002) phân tích một mẫu gồm 115 thành phố tự trị (42 trong số đó đã nhận được trợ cấp). Dubois và Fattore (2011) sử dụng mô hình tobit để điều tra vai trò của các yếu tố khác nhau trong việc nhận quỹ của Liên minh Châu Âu bằng cách áp dụng các chính phủ cấp dưới của Ba Lan. Tuy nhiên, dữ liệu có thể bị kiểm duyệt ở một điểm cao hơn 0, với nguy cơ thông số kỹ thuật sai.
Cả hai nghiên cứu đều áp dụng Probit và các mô hình khác để kiểm tra tính mạnh mẽ. Mô hình Tobit cũng đã được áp dụng trong phân tích nhu cầu để phù hợp với các quan sát với chi phí bằng không đối với một số hàng hóa.
Trong một ứng dụng liên quan của mô hình tobit, một hệ thống các mô hình hồi quy tobit phi tuyến đã được sử dụng để cùng ước tính một hệ thống nhu cầu thương hiệu với các biến phương sai thay đổi, phương sai, phương sai và tổng quát.
3. Mô hình bị cắt bỏ (Truncated Model)
Trong các mẫu của mô hình bị cắt bỏ (truncated model) nếu bạn không có thông tin về biến phụ thuộc, thì bạn không thể thu thập được thông tin về các biến giải thích mà các biến đó có thể có quan hệ với biến phụ thuộc.
Cụ thể, ví dụ về bộ dữ liệu đã bàn ở mô hình Tobit về quyết định gửi tiền + lượng tiền sẽ gửi vào ngân hàng thì khi khách hàng không gửi tiết kiệm thì điều này sẽ dẫn đến bạn không nắm được lượng tiền họ gửi là bao nhiêu cùng với việc các biến giải thích khác như THUONGHIEU, NGUOITHAN thì làm sao bạn biết được vì họ đâu có quyết định gửi tiền để mà hỏi tiếp chẳng hạn.
3.1. So sánh Mô hình hồi quy “cắt bỏ” (truncated) & Mô hình hồi quy “kiểm duyệt” (censored)
Trong kinh tế lượng, dữ liệu “censored” hay “truncated” là hoàn toàn khác biệt. Dữ liệu bị “kiểm duyệt” (censored) xảy ra khi biến phụ thuộc đã bị “kiểm duyệt” (censored) tại một điểm tham chiếu nào đó sao cho các giá trị bên trên (above) hay bên dưới (below) giá trị tham chiếu là không thể quan sát được như đã bàn luận phía bên trên.
Ngược lại dữ liệu sẽ được gọi là “bị cắt bỏ” khi các quan sát cho cả biến phụ thuộc và biến độc lập đều bị mất khi biến phụ thuộc ở trên hay ở dưới một ngưỡng giới hạn nào đó.
Do vậy sự khác biệt chính của dữ liệu “bị cắt bỏ” so với dự liệu “bị kiểm duyệt” là chúng ta không thể quan sát được biến phụ thuộc yi và cả biến giải thích xi khi một số quan sát bị cắt bỏ mất hoàn toàn ra khỏi dữ liệu quán sát.
Funfact: Cả hai ông mô hình bị kiểm duyệt sử dụng phương pháp Tobit và mô hình bị cắt bỏ sử dụng phương pháp truncated thì đều được ước lượng đồng thời bởi phương pháp Maximum Likelihood (ML).
3.2. Hồi quy mô hình bị cắt bỏ (truncated regression model)
Lệnh chạy mô hình bị cắt bỏ như sau:
truncreg SOTIENGUI GIOITINH TUOI HONNHAN HOCVAN THUNHAP KHOANGCACH NGUOITHAN THUONGHIEU, ll(1) ul(5)Kết quả:
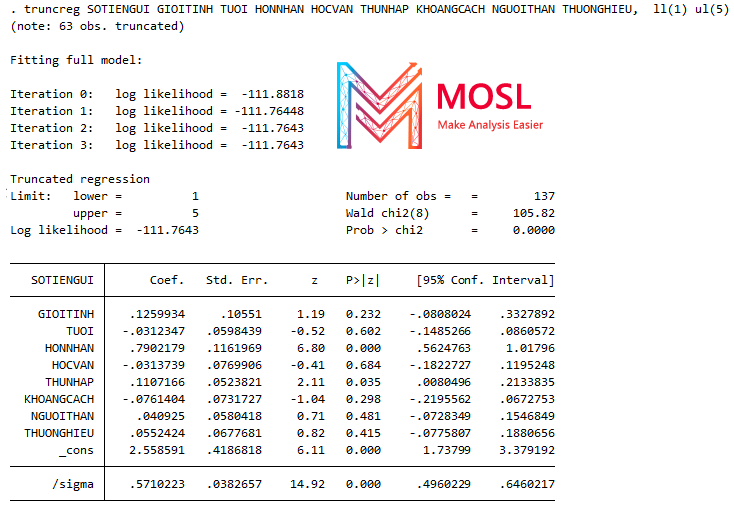
Giải thích: Tương tự như tobit chỉ thay lệnh đầu bằng lệnh truncreg (nếu bị lỗi vì chưa cài lệnh này thì nhập: ssc install truncreg nha). Còn chặn trên và chặn dưới hay chặn trái và phải tuỳ bạn thích đọc thế nào thì cũng như chạy bên mô hình Tobit phía bên trên thôi nhé!
Việc giải thích kết quả hay chạy về tác động biên (marginal effect) thì đều có chung 1 cách giải thích như đã trình bày phía trên hồi quy mô hình Tobit.
FUNFACT: Bây giờ, giữa các mô hình hồi quy kiểm duyệt và bị xén, mô hình nào tốt hơn? Vì mô hình hồi quy Tobit sử dụng nhiều thông tin hơn mô hình hồi quy bị xén, nên các giá trị ước lượng có được từ mô hình Tobit được kỳ vọng hiệu quả hơn
3.3. Hồi quy Heckman cho biến phụ thuộc “bị cắt bỏ” (Truncated Dependent Variables)
Đối với mô hình bị cắt bỏ hay “truncated” thì mô hình tổng quát sẽ bao gồm 2 phương trình hồi quy:
- Một phương trình với các điểm rơi vào vùng dữ liệu bị cắt bỏ và phương trình còn lại để mô hình hoá các biến cho kết quả
- Phương trình thứ hai chính là phương pháp Tobit (Ngạc nhiên phải không nào)
Đến đây nếu bạn nghĩ để ước lượng mô hình bị cắt bỏ dạng cao cấp hơn thì phải dùng 1 ông hồi quy cắt bỏ + thêm 1 ông Tobit để làm đúng không?
- Câu trả lời là không vì các nhà nghiên cứu tin rằng các biến số trong mẫu dữ liệu thu thập và các phương trình ước lượng sẽ khác nhau:
- Vì vậy, phương pháp hồi quy 2 giai đoạn Heckman (1976) cho phép sự tự tương quan giữa các sai số hồi quy trong lúc ước lượng các phương trình tách biệt nhau như trên.
Sử dụng code sau để chạy hồi quy 2 giai đoạn Heckman:
heckman SOTIENGUI GIOITINH TUOI HONNHAN HOCVAN THUNHAP KHOANGCACH NGUOITHAN THUONG
HIEU, select(GUITK=KHOANGCACH NGUOITHAN THUONGHIEU) twostep
Kết quả:
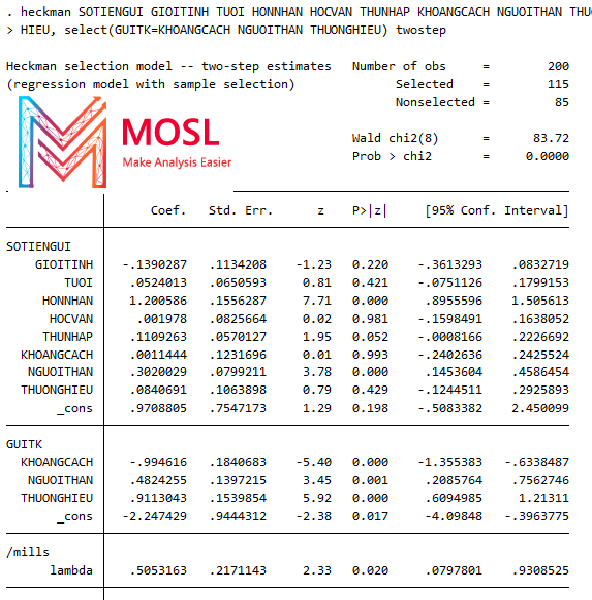
Giải thích: Lệnh select ở đây thêm những biến bị cắt bỏ do không quan sát được cụ thể như biến GUITK (tức quyết định gửi tiết kiệm nếu KH không gửi thì sẽ không quan sát được), biến khoảng cách, tác động của người thân, thương hiệu của ngân hàng đều là những biến không thể hỏi được khách hàng đó vì họ không có gửi tiết kiệm thì họ khó có thể trả lời được.
Cách giải thích mô hình bị cắt bỏ của Heckman này tương tự như mô hình Tobit đã bàn luận ở phía trên các bạn có thể nghiên cứu thêm nhé!
4. Tổng kết
Như vậy là MOSL đã đi qua các phần giời thiệu + cách chạy mô hình Tobit cùng hướng dẫn cực kỳ chi tiết và sâu sa để các bạn hiểu được rồi nhé!
Đến đây mong là các bạn nắm hết được các kiến thức trên, nếu có thắc mắc xin hãy để lại câu hỏi dưới phần bình luận để Mosl giải đáp liền nè.
MOSL xin chúc các bạn học tập và làm việc hiêu quả!
Xem thêm: Hỗ trợ chạy Stata của Mosl.vn
[su_box title=”Liên hệ: ” style=”glass” box_color=” #51d7bb “] Hotline: 0707.33.9698 hoặc Mail: sales@mosl.vn | Fanpage: Mentor Of Số Liệu – Mosl.vn . ĐIỀN THÔNG TIN ĐỂ NHẬN TƯ VẤN ngay Tại đây [/su_box]








