Chưa có sản phẩm trong giỏ hàng!
Phân tích tương quan Pearson và Spearman trong SPSS: Hướng dẫn A-Z 2025

Bạn từng bối rối trước một bảng số liệu phức tạp chưa? Đặc biệt khi cần tìm hiểu mối quan hệ giữa hai biến số trong nghiên cứu khoa học. Phân tích tương quan là công cụ không thể thiếu giúp bạn khám phá những mối liên hệ ẩn giấu trong dữ liệu.
SPSS (Statistical Package for the Social Sciences) cung cấp hai phương pháp tương quan mạnh mẽ: Pearson và Spearman. Mỗi phương pháp có ưu điểm riêng, phù hợp với từng loại dữ liệu cụ thể. Hiểu rõ sự khác biệt giữa chúng sẽ giúp bạn đưa ra kết luận chính xác cho nghiên cứu của mình.
Bài viết này sẽ hướng dẫn chi tiết từng bước thực hiện phân tích tương quan Pearson và Spearman trong SPSS 2025. Từ việc chuẩn bị dữ liệu, chạy phân tích, đến diễn giải kết quả một cách chuyên nghiệp. Đặc biệt, MOSL sẽ chia sẻ những mẹo thiết thực giúp bạn tránh những sai lầm phổ biến.
Kết thúc bài viết, bạn sẽ tự tin thực hiện phân tích tương quan cho luận văn, báo cáo nghiên cứu hay dự án công việc. Hãy cùng bắt đầu hành trình làm chủ dữ liệu này nhé!
1. Phân tích tương quan là gì và tại sao quan trọng trong SPSS?

Phân tích tương quan đo lường mức độ liên quan giữa hai biến số trong nghiên cứu. Đây là bước đầu quan trọng giúp nhà nghiên cứu khám phá mối quan hệ tiềm ẩn. Không giống như phân tích hồi quy, tương quan không xác định quan hệ nhân quả mà chỉ đo lường sự đồng biến.
Khi số liệu tăng ở biến này, liệu biến kia có tăng theo không? Hay ngược lại, khi biến này tăng thì biến kia giảm? Đó chính là những câu hỏi mà phân tích tương quan giải đáp. Hệ số tương quan dao động từ -1 đến +1, cho biết cả hướng và cường độ mối quan hệ.
Định nghĩa cốt lõi: Phân tích tương quan là phương pháp thống kê đo lường mức độ và hướng của mối quan hệ tuyến tính hoặc phi tuyến giữa hai biến liên tục hoặc thứ bậc.
SPSS đặc biệt mạnh trong phân tích tương quan nhờ giao diện thân thiện và khả năng xử lý dữ liệu lớn. Phần mềm này tự động tính toán các hệ số tương quan, kiểm định ý nghĩa thống kê và tạo báo cáo chi tiết. Điều này giúp các nhà nghiên cứu tiết kiệm thời gian và giảm thiểu sai sót trong tính toán.
1.1 Tầm quan trọng của phân tích tương quan trong nghiên cứu hiện đại
Phân tích tương quan đóng vai trò nền tảng trong hầu hết nghiên cứu thực nghiệm:
• Khám phá mối quan hệ ban đầu: Xác định biến nào có liên quan trước khi thực hiện phân tích phức tạp hơn
• Kiểm tra giả thuyết nghiên cứu: Xác minh các quan hệ lý thuyết được đề xuất
• Lựa chọn biến cho mô hình: Giúp quyết định biến nào nên đưa vào phân tích hồi quy
• Kiểm tra đa cộng tuyến: Phát hiện tương quan cao giữa các biến độc lập có thể gây vấn đề
Theo nghiên cứu thực tế, hơn 80% các bài báo khoa học sử dụng ít nhất một dạng phân tích tương quan. Đây là minh chứng cho tầm quan trọng không thể phủ nhận của phương pháp này trong nghiên cứu hiện đại.
2. So sánh tổng quan: Pearson vs Spearman trong SPSS
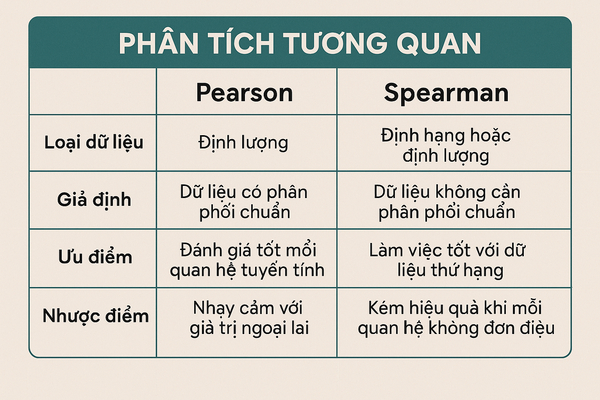
Lựa chọn giữa Pearson và Spearman phụ thuộc vào loại dữ liệu và mục tiêu phân tích cụ thể. Hiểu rõ sự khác biệt giúp bạn đưa ra quyết định chính xác. Cả hai phương pháp đều có vị trí riêng trong nghiên cứu khoa học.
Pearson đo lường mối quan hệ tuyến tính giữa hai biến liên tục có phân phối chuẩn. Spearman phù hợp với dữ liệu thứ bậc hoặc không tuân theo phân phối chuẩn. Cả hai đều được tích hợp sẵn trong SPSS với giao diện dễ sử dụng.
| Tiêu chí | Pearson | Spearman |
|---|---|---|
| Loại dữ liệu | Biến liên tục, định lượng | Biến thứ bậc, không chuẩn |
| Phân phối dữ liệu | Yêu cầu phân phối chuẩn | Không yêu cầu phân phối chuẩn |
| Mối quan hệ đo lường | Tuyến tính | Monotonic (đơn điệu) |
| Nhạy cảm với outlier | Rất nhạy cảm | Ít nhạy cảm |
| Cường độ tương quan | r từ -1 đến +1 | ρ (rho) từ -1 đến +1 |
| Ưu điểm chính | Chính xác cho dữ liệu chuẩn | Linh hoạt, robust |
| Ứng dụng phổ biến | Khoa học tự nhiên, kinh tế | Khoa học xã hội, y tế |
2.1 Bảng so sánh nhanh Pearson và Spearman
Pearson phù hợp khi dữ liệu có phân phối chuẩn và mối quan hệ tuyến tính rõ ràng. Spearman là lựa chọn an toàn khi không chắc chắn về phân phối dữ liệu. Trong thực tế, nhiều nhà nghiên cứu chạy cả hai phương pháp để so sánh kết quả.
Khi kết quả Pearson và Spearman khác nhau đáng kể, điều này có thể báo hiệu dữ liệu không tuân theo phân phối chuẩn. Spearman thường được ưa chuộng trong nghiên cứu khoa học xã hội do tính linh hoạt cao.
3. Phân tích tương quan Pearson trong SPSS
Hệ số tương quan Pearson (ký hiệu r) đo lường mức độ mối quan hệ tuyến tính giữa hai biến định lượng. Phương pháp này được Karl Pearson phát triển vào đầu thế kỷ 20. Pearson correlation đặc biệt hiệu quả khi dữ liệu tuân theo phân phối chuẩn.
Tương quan Pearson giả định rằng mối quan hệ giữa hai biến là đường thẳng. Nếu biến X tăng một đơn vị, biến Y sẽ tăng hoặc giảm một lượng tương ứng. Điều này làm cho Pearson rất phù hợp cho dữ liệu khoa học tự nhiên và kinh tế.
Trong SPSS, việc thực hiện tương quan Pearson SPSS trở nên đơn giản với giao diện click-and-run. Phần mềm tự động kiểm tra các giả định cơ bản và cung cấp kết quả chi tiết. Bạn có thể dễ dàng xuất kết quả thành bảng định dạng APA chuẩn.
Formula toán học của Pearson: r = Σ[(Xi – X̄)(Yi – Ȳ)] / √[Σ(Xi – X̄)² × Σ(Yi – Ȳ)²]. Tuy nhiên, bạn không cần tính toán thủ công khi có SPSS hỗ trợ. Hiểu công thức giúp bạn nắm vững bản chất của phương pháp này.
3.1 Điều kiện và giả định của phân tích Pearson

Trước khi thực hiện phân tích Pearson, cần kiểm tra các điều kiện sau:
1. Dữ liệu định lượng liên tục
Cả hai biến phải là số liệu đo lường trên thang tỷ lệ hoặc khoảng cách. Ví dụ: điểm số, thu nhập, chiều cao, cân nặng. Dữ liệu thứ bậc (như mức độ hài lòng 1-5) không phù hợp cho Pearson.
2. Phân phối chuẩn
Mỗi biến nên có phân phối tiệm cận chuẩn. Trong SPSS, bạn có thể kiểm tra bằng biểu đồ histogram hoặc kiểm định Shapiro-Wilk. Nếu dữ liệu lệch đáng kể, nên cân nhắc chuyển sang Spearman.
3. Mối quan hệ tuyến tính
Biểu đồ scatter plot phải thể hiện xu hướng đường thẳng rõ ràng. Mối quan hệ cong hoặc phi tuyến sẽ làm giảm độ chính xác của Pearson. SPSS cho phép tạo scatter plot một cách nhanh chóng để đánh giá.
4. Không có outlier nghiêm trọng
Các giá trị bất thường có thể làm méo kết quả tương quan Pearson. Sử dụng boxplot trong SPSS để phát hiện outlier. Cân nhắc loại bỏ hoặc biến đổi các giá trị này trước khi phân tích.
3.2 Hướng dẫn thực hiện Pearson correlation trong SPSS từng bước
Bước 1: Chuẩn bị dữ liệu
Mở file dữ liệu trong SPSS và kiểm tra cấu trúc dữ liệu. Đảm bảo các biến cần phân tích đã được định nghĩa đúng loại (Scale). Nếu chưa biết cách nhập dữ liệu từ Excel vào SPSS, bạn có thể tham khảo hướng dẫn chi tiết của MOSL.
Bước 2: Kiểm tra điều kiện phân tích
Tạo histogram cho từng biến: Graphs → Chart Builder → Histogram. Kiểm tra phân phối có tiệm cận chuẩn không. Tạo scatter plot để đánh giá mối quan hệ tuyến tính: Graphs → Chart Builder → Scatter/Dot.
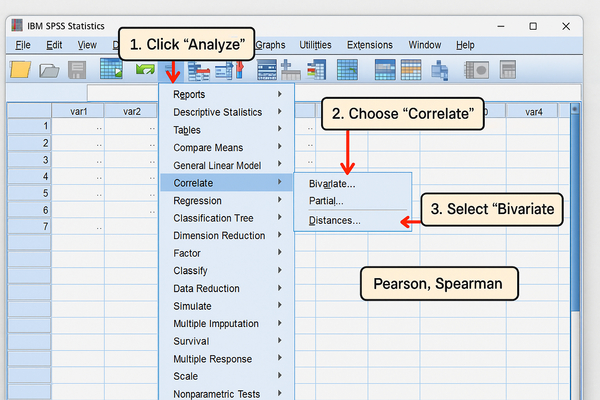
Bước 3: Truy cập menu phân tích
Chọn menu Analyze → Correlate → Bivariate. Đây là đường dẫn chuẩn để thực hiện phân tích tương quan trong SPSS 2025. Cửa sổ Bivariate Correlations sẽ hiện ra với nhiều tùy chọn.
Bước 4: Lựa chọn biến phân tích
Chuyển các biến cần phân tích từ ô Variables sang ô Variables to Correlate. Bạn có thể chọn nhiều biến cùng lúc để tạo ma trận tương quan. SPSS sẽ tự động tính tương quan giữa tất cả cặp biến.
Bước 5: Thiết lập tùy chọn Pearson
Trong phần Correlation Coefficients, đảm bảo đã chọn Pearson. Phần Test of Significance chọn Two-tailed nếu không có giả thuyết về hướng tương quan. Tích chọn Flag significant correlations để đánh dấu kết quả có ý nghĩa.
Bước 6: Chạy phân tích
Nhấn OK để thực hiện phân tích. SPSS sẽ xử lý và hiển thị kết quả trong cửa sổ Output. Quá trình này thường diễn ra rất nhanh, ngay cả với bộ dữ liệu lớn.
3.3 Đọc và diễn giải kết quả Pearson correlation
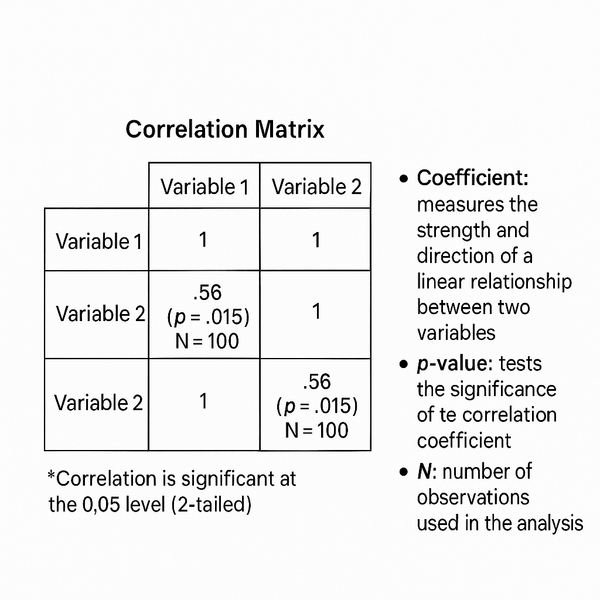
Kết quả Pearson correlation trong SPSS được trình bày dưới dạng ma trận tương quan. Mỗi ô chứa ba thông tin quan trọng: hệ số tương quan r, mức ý nghĩa (p-value), và số quan sát (N). Hiểu cách đọc ma trận này là chìa khóa để diễn giải chính xác.
Đọc hệ số tương quan r:
Giá trị r dao động từ -1 đến +1. Càng gần ±1, mối quan hệ càng mạnh. r = 0 nghĩa là không có mối quan hệ tuyến tính. Dấu của r cho biết hướng: dương là quan hệ cùng chiều, âm là ngược chiều.
Diễn giải p-value:
P-value cho biết khả năng kết quả xảy ra do ngẫu nhiên. Thông thường, p < 0.05 được coi là có ý nghĩa thống kê. SPSS đánh dấu * cho p < 0.05 và ** cho p < 0.01, giúp nhận biết nhanh chóng.
Báo cáo kết quả theo chuẩn APA:
“Có tương quan dương có ý nghĩa thống kê giữa điểm Toán và điểm Lý (r = .743, p < .001, N = 150).” Luôn báo cáo đầy đủ ba thành phần này trong nghiên cứu khoa học.
Lưu ý quan trọng:
Ma trận tương quan có tính đối xứng. Tương quan từ biến A đến B bằng tương quan từ B đến A. Đường chéo chính luôn có r = 1.000 vì mỗi biến tương quan hoàn hảo với chính nó.
4. Phân tích tương quan Spearman trong SPSS
Hệ số tương quan Spearman (ký hiệu ρ – rho) đo lường mức độ mối quan hệ monotonic giữa hai biến. Charles Spearman phát triển phương pháp này như một giải pháp robust thay thế cho Pearson. Spearman correlation SPSS đặc biệt phổ biến trong nghiên cứu khoa học xã hội và y tế.
Khác với Pearson, Spearman sử dụng thứ hạng (rank) của giá trị thay vì giá trị gốc. Điều này làm cho phương pháp ít bị ảnh hưởng bởi outlier và phân phối không chuẩn. Spearman có thể phát hiện mối quan hệ cong, miễn là quan hệ đó mang tính đơn điệu.
Trong SPSS, việc thực hiện Spearman correlation gần như tương tự Pearson. Bạn chỉ cần thay đổi một checkbox trong cùng menu Bivariate Correlations. Điều này giúp so sánh trực tiếp kết quả hai phương pháp một cách thuận tiện.
Spearman phù hợp với dữ liệu thứ bậc như thang Likert (1-5 điểm). Phương pháp này cũng xử lý tốt dữ liệu có phân phối lệch hoặc chứa nhiều outlier. Đây là lựa chọn an toàn khi không chắc chắn về tính chất phân phối.
4.1 Điều kiện áp dụng phân tích Spearman
Dữ liệu thứ bậc hoặc không tuân theo phân phối chuẩn:
Spearman chấp nhận dữ liệu ordinal như xếp hạng, đánh giá mức độ hài lòng. Cũng phù hợp với dữ liệu định lượng có phân phối lệch. Điều này làm cho Spearman trở nên linh hoạt hơn Pearson đáng kể.
Mối quan hệ monotonic:
Không yêu cầu mối quan hệ phải tuyến tính hoàn toàn. Chỉ cần khi một biến tăng, biến kia có xu hướng tăng (hoặc giảm) một cách nhất quán. Quan hệ có thể là đường cong, miễn là không thay đổi hướng.
Có outlier trong dữ liệu:
Spearman ít nhạy cảm với các giá trị bất thường. Trong khi outlier có thể làm méo kết quả Pearson, chúng ít ảnh hưởng đến Spearman. Đây là ưu điểm lớn trong phân tích dữ liệu thực tế.
So sánh với điều kiện Pearson:
Khi dữ liệu không đáp ứng đầy đủ điều kiện Pearson, Spearman là lựa chọn thay thế tốt. Nhiều nhà nghiên cứu chọn Spearman như phương pháp mặc định để tránh vi phạm giả định.
4.2 Hướng dẫn thực hiện Spearman correlation trong SPSS
Các bước tương tự Pearson với điều chỉnh:
Menu Analyze → Correlate → Bivariate vẫn là đường dẫn chính. Chọn biến cần phân tích vào ô Variables. Điểm khác biệt chính nằm ở phần Correlation Coefficients.
Chọn Spearman thay vì Pearson:
Trong phần Correlation Coefficients, bỏ tick Pearson và tick chọn Spearman. SPSS cho phép chọn cả hai cùng lúc để so sánh kết quả. Điều này rất hữu ích khi muốn đánh giá tính robust của kết quả.
Thiết lập tùy chọn kiểm định:
Giữ nguyên Two-tailed test trừ khi có giả thuyết định hướng cụ thể. Flag significant correlations giúp dễ dàng nhận biết kết quả có ý nghĩa. Các tùy chọn khác tương tự như Pearson.
Lưu ý đặc biệt cho SPSS 2025:
Phiên bản mới có giao diện được cải tiến với tooltips chi tiết. Bootstrap options cho phép tính khoảng tin cậy robust cho hệ số tương quan. Missing values handling cũng được cải thiện đáng kể.
4.3 Đọc và diễn giải kết quả Spearman correlation
Hiểu hệ số Spearman ρ (rho):
Giống như Pearson, rho dao động từ -1 đến +1. Tuy nhiên, ý nghĩa khác biệt: rho đo lường mức độ mối quan hệ monotonic, không nhất thiết tuyến tính. Rho = 0.8 có nghĩa 80% cặp quan sát theo thứ tự monotonic.
So sánh với kết quả Pearson:
Khi chạy cả hai phương pháp trên cùng dữ liệu, so sánh r và ρ. Nếu khác biệt lớn, có thể dữ liệu không tuân theo phân phối chuẩn hoặc mối quan hệ không tuyến tính. Spearman thường tin cậy hơn trong trường hợp này.
Báo cáo kết quả Spearman:
“Phân tích Spearman cho thấy tương quan rank dương có ý nghĩa giữa thứ hạng lương và thứ hạng hài lòng công việc (ρ = .652, p < .01, N = 200).” Sử dụng ký hiệu ρ thay vì r để phân biệt.
Ưu điểm trong diễn giải:
Spearman dễ giải thích với dữ liệu thứ bậc. Không cần lo lắng về phân phối dữ liệu hay outlier. Kết quả Spearman thường ổn định hơn khi lặp lại nghiên cứu với mẫu khác.
5. Tạo và đọc ma trận tương quan trong SPSS
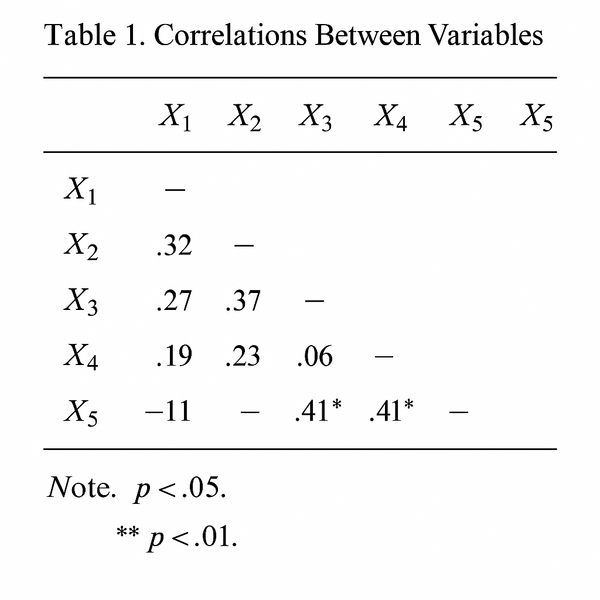
Ma trận tương quan SPSS là bảng hiển thị hệ số tương quan giữa tất cả cặp biến trong phân tích. Đây là công cụ mạnh mẽ giúp nhà nghiên cứu nhanh chóng nắm bắt toàn cảnh mối quan hệ giữa các biến. SPSS tự động tạo ma trận đối xứng với đường chéo chính luôn bằng 1.0.
Khi phân tích nhiều biến cùng lúc, ma trận tương quan trở nên vô cùng hữu ích. Thay vì kiểm tra từng cặp biến riêng lẻ, bạn có thể quan sát tất cả trong một bảng duy nhất. Điều này đặc biệt quan trọng khi nghiên cứu có 5-10 biến trở lên.
Cách tạo ma trận cho nhiều biến:
Trong cửa sổ Bivariate Correlations, chọn tất cả biến quan tâm vào ô Variables. SPSS sẽ tự động tính tương quan cho tất cả cặp biến. Kết quả hiển thị dưới dạng ma trận tam giác trên hoặc ma trận đầy đủ.
Xử lý missing values:
SPSS cung cấp hai tùy chọn: Exclude cases pairwise (loại từng cặp) hoặc Exclude cases listwise (loại toàn bộ). Pairwise giữ lại nhiều dữ liệu hơn nhưng có thể tạo ra kết quả không nhất quán giữa các cặp biến.
Để hiểu rõ hơn về cách SPSS xử lý dữ liệu, bạn có thể tham khảo bài viết SPSS là gì để nắm vững kiến thức nền tảng.
5.1 Diễn giải ý nghĩa hệ số tương quan từ -1 đến +1
Phân loại cường độ tương quan theo Cohen (1988):
| Khoảng giá trị |r| | Cường độ | Diễn giải |
|---|---|---|
| 0.00 – 0.10 | Không đáng kể | Gần như không có mối quan hệ |
| 0.10 – 0.30 | Yếu | Mối quan hệ nhỏ |
| 0.30 – 0.50 | Vừa phải | Mối quan hệ trung bình |
| 0.50 – 0.70 | Mạnh | Mối quan hệ đáng kể |
| 0.70 – 0.90 | Rất mạnh | Mối quan hệ cao |
| 0.90 – 1.00 | Gần hoàn hảo | Mối quan hệ rất cao |
Ý nghĩa dấu của hệ số tương quan:
Dấu dương (+) cho biết quan hệ cùng chiều: khi biến này tăng, biến kia cũng tăng. Dấu âm (-) nghĩa là quan hệ ngược chiều: khi biến này tăng, biến kia giảm. Độ lớn của hệ số quan trọng hơn dấu trong việc đánh giá cường độ.
Benchmark theo ngành nghiên cứu:
Khoa học xã hội: r > 0.3 được coi là có ý nghĩa thực tế. Khoa học tự nhiên: thường yêu cầu r > 0.7 do độ chính xác đo lường cao hơn. Y học: r = 0.2-0.4 có thể có ý nghĩa lâm sàng quan trọng.
Lưu ý về coefficient của determination:
r² cho biết tỷ lệ phương sai được giải thích. Ví dụ: r = 0.6 nghĩa là r² = 0.36, tức 36% sự biến thiên của biến này giải thích được biến kia. Đây là thông tin quan trọng để đánh giá ý nghĩa thực tế.
5.2 Lưu ý quan trọng: Tương quan không phải quan hệ nhân quả
Nguyên tắc cơ bản: “Correlation ≠ Causation”
Đây là một trong những sai lầm phổ biến nhất trong nghiên cứu. Tương quan cao không có nghĩa biến này gây ra biến kia. Cần phân tích sâu hơn và thiết kế nghiên cứu phù hợp để khẳng định quan hệ nhân quả.
Các yếu tố confounding:
Biến thứ ba có thể ảnh hưởng đến cả hai biến được nghiên cứu. Ví dụ: tương quan giữa doanh số kem và số vụ đuối nước không có nghĩa kem gây đuối nước, mà cả hai đều tăng vào mùa hè.
Ví dụ điển hình về hiểu lầm:
Số lượng nhà thờ tương quan dương với tỷ lệ tội phạm trong thành phố. Điều này không có nghĩa nhà thờ gây tội phạm, mà do cả hai đều tăng theo quy mô dân số.
Cách trình bày đúng trong nghiên cứu:
“Kết quả cho thấy có tương quan dương giữa thời gian học tập và điểm số (r = .65, p < .001). Tuy nhiên, cần nghiên cứu thêm để xác định quan hệ nhân quả.” Luôn nhấn mạnh tính chất tương quan, không phải nhân quả.
6. Case study thực hành: So sánh Pearson và Spearman
MOSL sẽ hướng dẫn bạn thực hiện một case study hoàn chỉnh với dữ liệu thực tế về điểm số sinh viên. Bộ dữ liệu gồm 200 sinh viên với các biến: điểm Toán, điểm Lý, thời gian tự học, và đánh giá năng lực. Đây là ví dụ điển hình trong nghiên cứu giáo dục.
Mục tiêu case study là tìm hiểu mối quan hệ giữa thời gian học tập và kết quả học tập. Chúng ta sẽ thực hiện cả Pearson và Spearman trên cùng dữ liệu, sau đó so sánh kết quả. Điều này giúp hiểu rõ khi nào nên sử dụng phương pháp nào.
Đặc điểm dữ liệu mẫu:
Điểm Toán và Lý: thang 0-10, phân phối tiệm cận chuẩn. Thời gian tự học: giờ/tuần, có một số outlier do sinh viên học quá nhiều. Đánh giá năng lực: thang 1-5, dữ liệu thứ bậc điển hình.
Để chuẩn bị dữ liệu cho phân tích, bạn có thể tham khảo cách thống kê mô tả trong SPSS để kiểm tra đặc điểm phân phối trước khi chọn phương pháp phân tích.
6.1 Phân tích dữ liệu điểm số và thời gian học tập
Bước 1: Khám phá dữ liệu ban đầu
Tạo bảng thống kê mô tả cho tất cả biến: Analyze → Descriptive Statistics → Descriptives. Kiểm tra mean, standard deviation, minimum, maximum để nắm bắt đặc điểm dữ liệu. Chú ý các giá trị bất thường có thể ảnh hưởng kết quả.
Bước 2: Kiểm tra phân phối dữ liệu
Tạo histogram cho điểm Toán và Lý: Graphs → Legacy Dialogs → Histogram. Kết quả cho thấy phân phối tiệm cận chuẩn với một chút lệch phải. Thời gian học có phân phối lệch do một số sinh viên học rất nhiều.
Bước 3: Thực hiện phân tích Pearson
Analyze → Correlate → Bivariate, chọn Pearson cho điểm Toán, điểm Lý và thời gian học. Kết quả: r = 0.73 giữa điểm Toán-Lý (p < .001), r = 0.45 giữa thời gian học-điểm Toán (p < .001).
Bước 4: Thực hiện phân tích Spearman
Lặp lại phân tích nhưng chọn Spearman. Kết quả: ρ = 0.71 giữa điểm Toán-Lý (p < .001), ρ = 0.52 giữa thời gian học-điểm Toán (p < .001). Chú ý sự khác biệt trong tương quan thời gian-điểm.
So sánh và diễn giải:
Tương quan điểm Toán-Lý tương đương nhau (0.73 vs 0.71), cho thấy mối quan hệ tuyến tính tốt. Tương quan thời gian-điểm khác biệt (0.45 vs 0.52), gợi ý có yếu tố phi tuyến hoặc outlier ảnh hưởng Pearson.
Kết luận cho nghiên cứu:
Có mối quan hệ mạnh giữa điểm các môn học. Thời gian học có tương quan với kết quả, nhưng không hoàn toàn tuyến tính. Spearman cho kết quả robust hơn với dữ liệu thời gian học có outlier.
7. Xử lý lỗi và troubleshooting phổ biến
Trong quá trình thực hiện phân tích tương quan, bạn có thể gặp phải một số lỗi phổ biến. SPSS sẽ hiển thị thông báo cụ thể cho từng vấn đề. Hiểu và biết cách khắc phục những lỗi này sẽ giúp bạn tiết kiệm thời gian và có được kết quả chính xác.
Lỗi dữ liệu missing values:
SPSS hiển thị cảnh báo khi có quá nhiều missing values. Kiểm tra Pattern Analysis để xem missing có ngẫu nhiên không. Sử dụng Multiple Imputation nếu missing rate < 20%. Với missing rate cao, cân nhắc loại bỏ những cases có quá nhiều dữ liệu thiếu.
Warning về vi phạm giả định:
Khi dữ liệu không tuân theo phân phối chuẩn, SPSS có thể hiển thị warning. Sử dụng Shapiro-Wilk test để kiểm tra chính thức. Nếu p < 0.05, dữ liệu không chuẩn và nên chuyển sang Spearman hoặc biến đổi dữ liệu.
Output không hiển thị đúng:
Đôi khi ma trận tương quan hiển thị không đầy đủ hoặc bị lỗi format. Kiểm tra lại việc chọn biến và tùy chọn output. Restart SPSS nếu cần thiết. Đảm bảo phiên bản SPSS được cập nhật mới nhất.
Kết quả không hợp lý:
Tương quan = 1.000 hoặc rất gần 1 có thể do duplicate variables. Tương quan âm bất ngờ có thể do coding ngược. Kiểm tra lại định nghĩa biến và cách nhập liệu.
7.1 Mẹo và tricks nâng cao trong SPSS
Keyboard shortcuts hữu ích:
Ctrl+R để chạy lệnh syntax nhanh. Ctrl+D để duplicate analysis với thiết lập tương tự. F1 để mở help ngay trong dialog box. Những phím tắt này giúp tăng tốc độ làm việc đáng kể.
Customization output tables:
Double-click vào bảng output để edit format. Thay đổi số decimal places, font size, colors để phù hợp với yêu cầu báo cáo. Create custom table template để tái sử dụng cho nhiều phân tích.
Export kết quả chuyên nghiệp:
File → Export → Excel để xuất bảng có thể edit. Copy special → Rich Text Format để paste vào Word giữ nguyên format. Sử dụng OMS (Output Management System) để tự động xuất kết quả theo format định sẵn.
Integration với software khác:
SPSS Statistics Syntax có thể được save và chạy batch. Integration với R thông qua SPSS-R plugin. API connection với Python cho advanced analysis. Điều này mở rộng khả năng phân tích beyond SPSS interface.
Nếu bạn quan tâm đến việc kiểm tra độ tin cậy của thang đo trước khi phân tích tương quan, hãy tham khảo hướng dẫn kiểm định Cronbach’s Alpha trong SPSS để đảm bảo chất lượng dữ liệu.
Kết luận
Phân tích tương quan Pearson và Spearman trong SPSS là kỹ năng nền tảng mà mọi nhà nghiên cứu cần thành thạo. Qua bài viết này, bạn đã được trang bị kiến thức toàn diện từ lý thuyết đến thực hành. Từ việc hiểu bản chất của từng phương pháp, đến cách chọn lựa phù hợp với loại dữ liệu cụ thể.
SPSS 2025 đã làm cho quá trình phân tích tương quan trở nên đơn giản và trực quan hơn bao giờ hết. Bạn có thể tự tin thực hiện phân tích cho luận văn, nghiên cứu khoa học hay báo cáo công việc. Điều quan trọng là luôn kiểm tra các giả định trước khi phân tích và diễn giải kết quả một cách thận trọng.
Hãy nhớ rằng tương quan không có nghĩa là quan hệ nhân quả. Đây là nguyên tắc vàng trong nghiên cứu khoa học. Sử dụng kết quả tương quan như bước đầu để khám phá mối quan hệ, sau đó áp dụng các phương pháp phân tích nâng cao hơn để kiểm định giả thuyết.
MOSL luôn đồng hành cùng bạn trong hành trình làm chủ dữ liệu. Với hơn 10 năm kinh nghiệm trong lĩnh vực phân tích số liệu, chúng tôi hiểu rõ những thách thức mà sinh viên và người đi làm gặp phải. Từ việc thiếu kiến thức nền tảng đến áp lực thời gian hoàn thành dự án.
Ib ngay cho MOSL để nhận thông tin tư vấn bằng cách liên hệ Hotline/Zalo: 0707339698. Đội ngũ chuyên gia của chúng tôi sẵn sàng hỗ trợ bạn với dịch vụ SPSS, dịch vụ Stata, dịch vụ thu thập dữ liệu khảo sát và dịch vụ hỗ trợ luận văn.
Để cập nhật thêm nhiều kiến thức hữu ích về phân tích dữ liệu và nghiên cứu khoa học, hãy theo dõi fanpage của MOSL tại https://www.facebook.com/mosl.group.
Các câu hỏi thường được quan tâm bao gồm:
Khi nào nên chọn Pearson thay vì Spearman? Pearson phù hợp khi dữ liệu có phân phối chuẩn và quan hệ tuyến tính rõ ràng. Spearman an toàn hơn khi không chắc chắn về phân phối hoặc có outliers trong dữ liệu.
Hệ số tương quan bao nhiêu được coi là mạnh? Theo Cohen (1988), |r| > 0.5 được coi là tương quan mạnh trong khoa học xã hội. Tuy nhiên, chuẩn này có thể khác tùy theo lĩnh vực nghiên cứu cụ thể.
*Làm sao biết kết quả có ý nghĩa thống kê? Kiểm tra p-value trong output SPSS. Nếu p < 0.05, kết quả có ý nghĩa thống kê. SPSS tự động đánh dấu * cho p < 0.05 và ** cho p < 0.01.*
Tại sao kết quả Pearson và Spearman khác nhau? Sự khác biệt lớn thường do dữ liệu không tuân theo phân phối chuẩn, có outliers, hoặc mối quan hệ không hoàn toàn tuyến tính. Trong trường hợp này, Spearman thường đáng tin cậy hơn.
Có nên loại bỏ outliers trước khi phân tích? Cần xem xét kỹ bản chất của outliers. Nếu là lỗi nhập liệu, nên sửa chữa. Nếu là giá trị thực, cân nhắc sử dụng Spearman thay vì loại bỏ.
Tương quan cao có nghĩa là có quan hệ nhân quả không? Không. Tương quan chỉ đo lường mức độ liên quan, không chứng minh quan hệ nhân quả. Cần thiết kế nghiên cứu thử nghiệm để khẳng định nhân quả.
Tài liệu tham khảo từ các nguồn uy tín:
Field, A. (2018). Discovering Statistics Using IBM SPSS Statistics (5th ed.). Sage Publications – Sách giáo khoa toàn diện về SPSS với nhiều ví dụ thực hành.
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.). Lawrence Erlbaum Associates – Nguồn tham khảo chuẩn cho việc diễn giải cường độ tương quan.
Pallant, J. (2020). SPSS Survival Manual: A Step by Step Guide to Data Analysis Using IBM SPSS (7th ed.). – Hướng dẫn từng bước dễ hiểu cho người mới bắt đầu.
IBM SPSS Statistics Documentation – Tài liệu chính thức từ nhà phát triển với updates mới nhất.
Chủ đề mở rộng:
Phân tích tương quan từng phần (Partial correlation) – Kiểm soát ảnh hưởng của biến thứ ba khi tính tương quan.
Tương quan phi tham số khác – Kendall’s tau-b cho dữ liệu có nhiều ties.
Phân tích tương quan đa biến – MANOVA và canonical correlation cho nhiều biến phụ thuộc.
Bootstrap confidence intervals – Tính khoảng tin cậy robust cho hệ số tương quan.
Các thuật ngữ liên quan cần biết:
Bivariate correlation – Tương quan giữa hai biến số.
Multicollinearity – Hiện tượng các biến độc lập có tương quan cao với nhau.
Effect size – Cường độ ảnh hưởng thực tế, ở đây là hệ số tương quan.
Statistical significance – Ý nghĩa thống kê, thường là p < 0.05.
Coefficient of determination – r², tỷ lệ phương sai được giải thích.
Outliers – Giá trị bất thường có thể ảnh hưởng kết quả phân tích.
Normality assumption – Giả định phân phối chuẩn cần thiết cho Pearson correlation.










