Đánh giá mức độ phù hợp của mô hình hồi quy trên R là điều cần thiết để kiểm tra xem mô hình có thật sự phù hợp với nghiên cứu hay không và từ đó giúp bạn điều chỉnh, sửa đổi tác cấu trúc mô hình cho phù hợp.

Khi thực hiện các phân tích cũng như nghiên cứu, chúng ta có thể phải đưa ra quyết định lựa chọn mô hình nào là phù hợp. Hoặc chúng ta cũng cần phải đánh giá phẩm chất, độ phù hợp của mô hình chẳng hạn. Để làm điều này, trước hết chúng ta phải quyết định cần phải sử dụng những tiêu chí gì để đánh giá một mô hình là tốt hơn những mô hình khác cũng như chất lượng của một mô hình cụ thể.

Ví dụ, để lựa chọn một mô hình trong số các mô hình cạnh tranh nhau chúng ta phải dựa vào một loạt các yếu tố cũng như tiêu chí khác nhau.

1. Đánh giá mức độ phù hợp của mô hình hồi quy trên R bằng tiêu chí R2

Đây là hai tiêu chí đo lường mức độ phù hợp của mô hình (Measures of Fit).

Về cơ bản, nếu mô hình có R2 hoặc R2 hiệu chỉnh cao hơn là mô hình tốt hơn.

Theo Gujarati & Porter (2009), hạn chế của tiêu chí này là chỉ so sánh và đánh giá được các mô hình có:

• (1) biến phụ thuộc là giống nhau

• (2) có kích cỡ mẫu như nhau.

Điều này có nghĩa là không thể lấy R2 làm tiêu chuẩn để đánh giá hai mô hình sau:

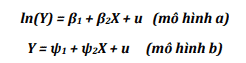
• Với hồi quy đơn (là mô hình chỉ có 1 biến độc lập) như ở mô hình a thì R2 = [cor(Y,X)]2 hay là bình phương tương quan giữa X và Y.

• Với hồi quy đa biến (mô hình có nhiều hơn 1 biến độc lập) thì R2 = [cor(Y,Ŷ )]2 trong đo ,Ŷ la gia trị dự báo của của Y thu được từ mô hình.

Giá trị tương quan càng cao thì ước lượng Y thu được càng gần với giá trị thực của nó,

Do đó mô hình nào có giá trị tương quan này cao hơn thì sẽ là mô hình tốt hơn.

2. Đánh giá mức độ phù hợp của mô hình hồi quy trên R theo phần dư

Sử dụng giá trị phần dư là tiêu chí sử dụng phổ biến khi so sánh, đánh giá mô hình.

Các tiêu chí theo phần dư thường có RMSE và MSE là hai tiêu chí sử dụng phổ biến hơn.

MSE được tính theo công thức sau:

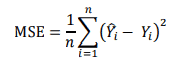
Còn RMSE được tính bằng căn bậc hai của MSE.
Một giá trị MSE (hoặc RMSE) càng bé thì có nghĩa là những giá trị ước lượng của Y sẽ càng sát với giá trị thực và do đó, một mô hình có MSE (RMSE) bé hơn sẽ là một mô hình tốt hơn.
Ngoài ra còn có các tiêu chí gồm MD, MAD, MPE và MAPE cũng có thể được sử dụng để đánh giá mô hình.

3. Các tiêu chuẩn thông tin AIC, SIC, và Cp của Mallow

Đây là nhóm tiêu chí thường được sử dụng để thay thế và hạn chế nhược điểm của R2
Với các kí hiệu các bạn đã quen thuộc, tiêu chuẩn thông tin Akaike (AIC) được tình theo công thức:

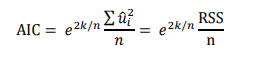
Với chú ý rằng n là số quan sát, k là số biến số trong mô hình.

Căn cứ vào tiêu chuẩn thông tin Akaike AIC, mô hình có AIC thấp hơn sẽ được lựa chọn. Hầu hết các phần mềm thống kê, kể cả R đều báo cáo tiêu chuẩn thông tin này.

Để có tiêu chuẩn thông tin Akaike các bạn sử dụng câu lệnh:

Tương tự, tiêu chuẩn thông tin Schwarz (SIC) cũng được sử dụng để đánh giá mô hình

Hiện tại, trong R chưa có sẵn hàm tính SIC nhưng có thể chạy SIC trong R như trên

SIC được tính theo công thức sau:

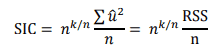
Một tiêu chuẩn nữa là hệ số Cp của Mallow (Mallow’s Cp Criterion) được tính theo công thức:

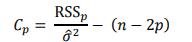
Trong đó p là số biến độc lập (chú ý với mô hình k biến thì p = k – 1).

Do vậy, chúng ta có thể xấp xỉ E(Cp) như sau:

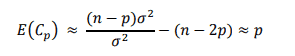
Căn cứ theo tiêu chí Cp, chúng ta sẽ ưu tiên lựa chọn mô hình có Cp thấp hơn

Và chọn mô hình có hệ số R2 hoặc R2 hiệu chỉnh càng cao càng tốt.

4. Tỉ lệ sai sót huấn luyện, sai sót kiểm định và hiện tượng quá khớp

Những gì các bạn sắp đọc chắc chắn là một thử thách.

Thông thường việc so sánh chất lượng giữa hai mô hình hình cạnh tranh nhau hoặc đánh giá chất lượng của một mô hình chúng ta thường dựa vào, chẳng hạn, tiêu chí R2 hoặc MSE.

Nếu chọn MSE để đánh giá thì mô hình nào có MSE bé hơn sẽ là mô hình tốt hơn.

Trong tình huống đặc biệt, nếu MSE = 0 (tương đương với R2 =1) thì có nghĩa là chúng ta có một mô hình hoàn hảo với ngụ ý rằng các biến số giải thích 100% biến động của biến phụ thuộc.

Tương tự, khi đánh giá một mô hình chúng ta thường căn cứ vào R2 – chỉ số này càng cao càng tốt. Hoặc chúng ta ta căn cứ vào MSE – chỉ số này càng thấp càng tốt. Phải chăng, chẳng hạn, chỉ căn cứ vào MSE để đánh giá (hay so sánh) chất lượng của các mô hình là đủ?

Câu trả lời là không.

Để đánh giá chất lượng của một mô hình, theo James et al. (2013), cần căn cứ vào đồng thời cả hai tiêu chí:

• (1) sai số huấn luyện – training test error,

• (2) sai số kiểm định – testing test error.

Để làm rõ hai khái niệm này chúng ta trở lại với bộ số liệu ở mục CPS1988 đã sử dụng ở chương 3 nhằm ước lượng mô hình sau:

• Thay vì ước lượng mô hình 2 với tất cả 28155 quan sát thì ta chỉ ước lượng mô hình này với 16.000 quan sát mà thôi.
• Rõ ràng là có đến K= 28155!/[16000!⨉(28155-16000)!] cách lấy ra 16000 quan sát từ 28155 quan sát và do vậy chúng ta cũng có chừng đó cặp giá trị ước lượng của β1 và β2 cũng như MSE.
• Dưới đây là 2 bộ số liệu rút ra từ K bộ số liệu có 16000 quan sát:

Ở đây có thể thấy MSE1 thu được từ bộ dữ liệu data1 bé hơn MSE2 thu được từ data2.

MSE1 và MSE2 đã thu ở trên chính là tỉ lệ sai sót huấn luyện (training error rate).

Ở đây, bộ dữ liệu được sử dụng để xây dựng mô hình là data1 và data2 nên trong nghiên cứu thống kê và kinh tế lượng.

Chúng có tên gọi là: dữ liệu huấn luyện (training data, hoặc training set).

5. Kết luận

Dưới đây là một số kiểm định hồi quy để đánh giá độ phù hợp của mô hình hồi quy trên R

MOSL xin chúc các độc giả học tập và làm việc hiệu quả.

Xem thêm: Dịch vụ chạy R của Mosl.vn

Liên hệ:

Hotline: 0707.33.9698 hoặc Mail: sales@mosl.vn | Fanpage: Mentor Of Số Liệu – Mosl.vn

Tag:

Nguồn: Tác giả Nguyễn Chí Dũng