Phương sai là gì? Phương sai hay Variance là một thước đo khoảng cách chênh lệch giữa các số liệu trong một tập dữ liệu với nhau so với giá trị trung bình của tập dữ liệu được ký hiệu là σ2 trong thống kê.
Có hai khái niệm riêng biệt được gọi là “phương sai“:
- Một, như đã thảo luận ở trên, thì phương sai là một phần của phân phối xác suất lý thuyết và được xác định bởi một phương trình. Phương sai khác là đặc điểm của một tập hợp các quan sát chính là khi phương sai được tính toán từ các quan sát, những quan sát đó thường được đo từ một hệ thống trong thế giới thực. Nếu tất cả các quan sát có thể có của hệ thống đều có mặt thì phương sai tính toán được gọi là phương sai tổng thể.
Tuy nhiên, thông thường chỉ có một tập hợp con và phương sai được tính từ đây được gọi là phương sai mẫu (sample variance). Phương sai được tính toán từ một mẫu được coi là ước tính của phương sai tổng thể đầy đủ. Có nhiều cách để tính ước tính phương sai tổng thể, sẽ được Mosl thảo luận trong phần bên dưới.
- Hai, là loại phương sai có liên quan chặt chẽ với nhau. Để biết cách thực hiện, hãy xem xét rằng phân phối xác suất lý thuyết có thể được sử dụng như một bộ tạo các quan sát giả định. Nếu vô số quan sát được tạo ra bằng cách sử dụng một phân phối, thì phương sai mẫu được tính từ tập hợp vô hạn đó sẽ khớp với giá trị được tính bằng cách sử dụng phương trình phương sai của phân phối.
Tóm lại hãy theo chân Mosl xuống phần bên dưới để hiểu rõ hơn các khái niệm phương sai là gì? và công thức cũng như cách tính nó sẽ như thế nào nhé!
1. Phương sai là gì?
1.1. Khái niệm
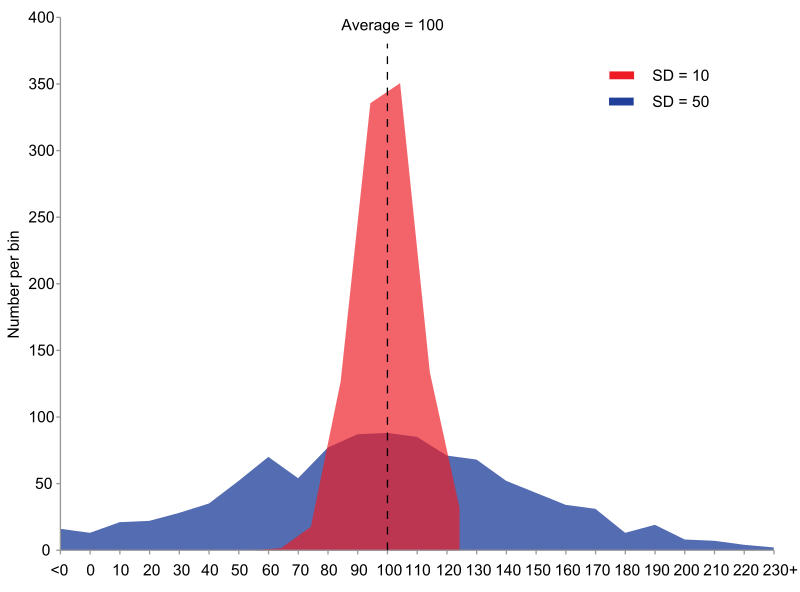
Phương sai tổng thể là khi phương sai được tính toán từ các quan sát mà các quan sát đó có mặt và được đo từ một hệ thống ở thế giới thực
Lưu ý: Khi phương sai được tính toán từ một phương sai mẫu từ một tập hợp con thì được gọi là ước tính của phương sai tổng thể đầy đủ.
1.2. Ý nghĩa của phương sai là gì – Variance Meaning?
Ý nghĩa của phương sai là gì trong thống kê và phân tích thực nghiệm? Các ý nghĩa rất quan trọng gồm:
- Phương sai là thước đo độ phân tán , có nghĩa là nó là thước đo mức độ trải rộng của một tập hợp số so với giá trị trung bình của chúng.
- Phương sai có vai trò trung tâm trong thống kê, trong đó một số ý tưởng sử dụng nó bao gồm thống kê mô tả , suy luận thống kê , kiểm tra giả thuyết , mức độ phù hợp và lấy mẫu Monte Carlo.
- Phương sai là một công cụ quan trọng trong khoa học, nơi phân tích thống kê dữ liệu là phổ biến. Phương sai là bình phương của độ lệch chuẩn , thời điểm trung tâm thứ hai của phân phối và hiệp phương sai của biến ngẫu nhiên với chính nó.
Mosl sẽ bàn về khái niệm hiệp phương sai là gì và cách tính trong bài viết tại đây
1.3. Công thức tính phương sai là gì?
Công thức tính phương sai của một biến ngẫu nhiên X là giá trị kỳ vọng của độ lệch bình phương so với giá trị trung bình của X.
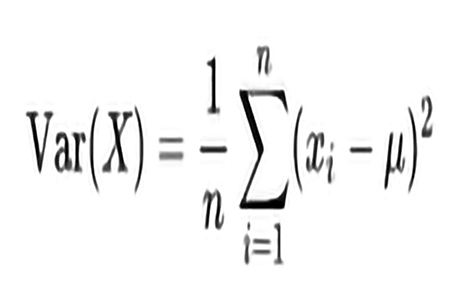
Tham khảo: Công thức tính độ lệch chuẩn là gì?
Định nghĩa này bao gồm các biến ngẫu nhiên được tạo ra bởi các quá trình rời rạc , liên tục , không hoặc hỗn hợp. Phương sai cũng có thể được coi là hiệp phương sai của một biến ngẫu nhiên với chính nó:
Trong đó:
xi là giá trị của quan sát thứ i
µ là giá trị trung bình của tập dữ liệu
n là số quan sát trong tập dữ liệu
N được tính trong tổng xích ma của xi
Giá trị x trung bình được tính bằng công thức trung bình tổng các quan sát.
Funfact: Căn bậc hai của phương sai là gì? Câu trả lời đó chính là độ lệch chuẩn (σ).
Xem thêm: Độ lệch chuẩn là gì? – What is standard deviation?
Bảng sau đây liệt kê phương sai của một số phân phối xác suất thường được sử dụng.
| Tên của phân phối xác suất | Hàm phân phối xác xuất | Nghĩa là | Phương sai |
| Phân phối nhị thức |  | np | np(1-p) |
| Phân bố hình học |  |  |  |
| Phân phối bình thường |  | µ | σ2 |
| Phân phối đồng đều (liên tục) |  b \ end {case}}}”> |  |  |
| Phân phối hàm mũ |  |  |  |
| Phân phối Poisson |  | λ | λ |
Cách bấm máy tính để tính phương sai cụ thể như hình dưới
Qua cách tính trên hình bằng máy tính casio fx570 trên hy vọng các bạn sẽ có thể giải được bài tập ước lượng kỳ vọng và phương sai trong xác xuất thống kê được rồi nè.
Cùng Mosl tìm hiểu thêm về Cách tính độ lệch chuẩn trong excel và máy tính casio fx570 nhé!
1.4. Thuộc tính cơ bản của phương sai
Dưới đấy là thống kê bảng thuộc tính của phương sai
| CÁC THUỘC TÍNH | Ý nghĩa công thức |
| Phương sai là không âm vì các bình phương là dương hoặc 0 | Var(X) ≥ 0 |
| Phương sai của một hằng số bằng không | Var(α) = 0 |
| Nếu phương sai của một biến ngẫu nhiên là 0, thì nó gần như chắc chắn là một hằng số |  |
| Phương sai là bất biến đối với những thay đổi trong tham số vị trí | Var(X + α) = Var(X) |
| Phương sai được chia tỷ lệ bình phương của một hằng số nào đó | Var(αX) = a2 Var(X) |
| Phương sai của tổng của hai biến ngẫu nhiên được cho bởi | Var(αX±bY) = α2Var(X) + b2Var(Y) + 2αbCov(X, Y) (Cov(X,Y) là hiệp phương sai) |
1.5. Các loại phương sai phổ biến
Trên thực tế có khá nhiều loại phương sai mà bạn cần biết như sau:
- Phương sai thu nhập: Đây là sự khác biệt giữa thu nhập thực tế và thu nhập kỳ vọng. Nếu con số thực tế cao hơn bạn mong đợi, phương sai được cho là có lợi. Nếu nó thấp hơn con số dự kiến, bạn có một phương sai bất lợi trong thu nhập.
- Phương sai chi phí: Điều này thể hiện sự khác biệt giữa chi phí thực tế và chi phí được lập ngân sách. Nếu bạn chi tiêu ít hơn ngân sách dự trù, sự khác biệt được cho là một phương sai có lợi; nếu bạn đã chi tiêu nhiều hơn dự toán, bạn có một phương sai bất lợi.
Bạn cũng có thể tính phương sai cho một loại chi phí cụ thể (ví dụ: chi phí vận chuyển và thực phẩm dự kiến và thực tế của bạn). Các doanh nghiệp thường theo dõi phương sai của các loại chi phí khác nhau, chẳng hạn như chi phí nguyên vật liệu trực tiếp hoặc chi phí lao động và chi phí chung.
- Phương sai thặng dư / thâm hụt hoặc lãi / lỗ: Một cá nhân cũng có thể chọn tính phương sai giữa thặng dư thực tế và thặng dư dự kiến, hoặc phương sai giữa thâm hụt thực tế hoặc dự kiến. Tương tự, một doanh nghiệp có thể chọn để đo lường phương sai giữa lãi hoặc lỗ thực tế và dự kiến.
2. Ưu và nhược điểm của phương sai
2.1. Ưu điểm của phương sai là gì?
Không thể không nhắc đến ưu điểm nổi bật của phương sai là:
- Phương sai như một thước đo độ phân tán là nó dễ dàng thao tác đại số hơn các thước đo độ phân tán khác như độ lệch tuyệt đối dự kiến.
Ví dụ: Phương sai của tổng các biến ngẫu nhiên không tương quan bằng tổng phương sai của chúng.
- Phương sai là nó xem tất cả các sai lệch so với giá trị trung bình giống nhau bất kể hướng của chúng, vì vậy chúng không bị triệt tiêu.
Bạn có biết: Thực tế phương sai không thể nào bằng 0 do không thể không có sự sai số nào trong một tập dữ liệu.
2.2. Nhược điểm của phương sai là gì?
Cũng phải biết được nhược điểm của phương sai là gồm các phần:
- Nhược điểm của phương sai đối với các ứng dụng thực tế là, không giống như độ lệch chuẩn, các đơn vị của nó khác với biến ngẫu nhiên, đó là lý do tại sao độ lệch chuẩn thường được báo cáo như một thước đo độ phân tán sau khi kết thúc tính toán.
- Phương sai làm tăng trọng số cho các dữ liệu ngoại lai, những dữ liệu ngoại lai có giá trị khác xa so với giá trị trung bình. Khi bình phương những giá trị này có thể sẽ làm lệch tập dữ liệu.
- Phương sai không dễ để diễn giải và người dùng phương sai thường sử dụng nó chủ yếu để lấy căn bậc hai của nó, hay độ lệch chuẩn của tập dữ liệu.
- Yếu tố lạm phát trong phương sai (Variance Inflation Factor).
3. Mở rộng phương sai tổng thể và phương sai mẫu
3.1. Phương sai tổng thể là gì?
Phương sai tổng thể khớp với phương sai của phân phối xác suất tạo ra.
Theo nghĩa này, khái niệm dân số của một tập hữu hạn dân số có kích thước N có thể được mở rộng cho các biến ngẫu nhiên liên tục với số lượng quần thể vô hạn.
3.2. Phương sai mẫu là gì?
3.2.1. Phương sai mẫu thiên vị là gì?
Trong nhiều tình huống thực tế, phương sai thực sự của một tập hợp không được biết trước và phải được tính toán bằng cách nào đó.
Khi xử lý các quần thể cực lớn, không thể đếm hết mọi đối tượng trong quần thể, vì vậy việc tính toán phải được thực hiện trên một mẫu của quần thể.
Để đưa ra một ước tính về phương sai tổng thể bị sai lệch bởi một hế số 
. Vì lý do này được gọi là phương sai mẫu thiên vị .
3.2.2. Phương sai mẫu không thiên vị là gì?
Việc sửa chữa độ chệch này tạo ra phương sai mẫu không chệch , được biểu thị 
![{\ displaystyle s ^ {2} = {\ frac {n} {n-1}} \ sigma _ {Y} ^ {2} = {\ frac {n} {n-1}} \ left [{\ frac {1} {n}} \ sum _ {i = 1} ^ {n} \ left (Y_ {i} - {\ overline {Y}} \ right) ^ {2} \ right] = {\ frac {1 } {n-1}} \ sum _ {i = 1} ^ {n} \ left (Y_ {i} - {\ overline {Y}} \ right) ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/522b961676ec2150e830c353fb27a42b4f45afdd "PHƯƠNG SAI là gì – Variance? Full Công thức & Cách tính #1 20")
Các ước lượng không thiên vị của độ lệch chuẩn là một vấn đề liên quan đến kỹ thuật, mặc dù đối với sự phân bố bình thường sử dụng thuật ngữ n – 1,5 sản lượng một ước lượng gần như không thiên vị.
Chú ý: Khi tính toán phương sai mẫu để ước tính phương sai tổng thể, mẫu số của phương trình phương sai tđược đổi thành (N – 1) để ước lượng không bị thiên vị và không đánh giá thấp phương sai tổng thể.
3.2.3. Phân phối phương sai mẫu là gì?
Là một hàm của các biến ngẫu nhiên, phương sai mẫu tự nó là một biến ngẫu nhiên, và việc nghiên cứu phân phối của nó là điều đương nhiên.
Trong trường hợp Y i là các quan sát độc lập từ phân phối chuẩn , định lý Cochran cho thấy s 2 tuân theo phân phối chi bình phương tỷ lệ.
![{\ displaystyle \ operatorname {E} \ left [s ^ {2} \ right] = \ sigma ^ {2}, \ quad \ operatorname {Var} \ left [s ^ {2} \ right] = {\ frac { \ sigma ^ {4}} {n}} \ left (\ kappa -1 + {\ frac {2} {n-1}} \ right) = {\ frac {1} {n}} \ left (\ mu _ {4} - {\ frac {n-3} {n-1}} \ sigma ^ {4} \ right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e1abcb2ddd063b31acc8ab73edee87d319f3e3c "PHƯƠNG SAI là gì – Variance? Full Công thức & Cách tính #1 21")
Nếu Y i là độc lập và được phân phối giống nhau, nhưng không nhất thiết phải được phân phối bình thường, thì trong đó κ là kurtosis của phân bố và μ 4 là thời điểm trung tâm thứ tư .
3.2.4. Sự bất bình đẳng của Samuelson
Bất đẳng thức Samuelson là một kết quả cho biết giới hạn trên các giá trị mà các quan sát riêng lẻ trong một mẫu có thể lấy, cho rằng giá trị trung bình của mẫu và phương sai (chệch) đã được tính toán.
Giá trị phải nằm trong giới hạn là:
4. Phương sai ứng dụng trong thực tế
4.1. Mômen quán tính trong vật lý
Phương sai của phân bố xác suất thống kê tương tự như mômen quán tính trong cơ học cổ điển về phân bố khối lượng tương ứng dọc theo một đường, liên quan đến chuyển động quay quanh khối tâm của nó.
Chính vì sự tương tự này mà những thứ như phương sai được gọi là mô men của phân phối xác suất. Ma trận hiệp phương sai có liên quan đến mômen quán tính của tensor đối với phân bố đa biến. Mômen quán tính của một đám mây gồm n điểm với ma trận hiệp phương sai là 
được đưa ra bởi
Các nhà vật lý sẽ coi đây là mômen thấp đối với trục x vì vậy mômen quán tính là
Funfact: Sự khác biệt này giữa mômen quán tính trong vật lý và trong thống kê là rõ ràng đối với các điểm được tập hợp dọc theo một đường thẳng.
4.2. Trong đầu tư
Phương sai được khá nhiều nhà phân tích áp dụng trong đầu tư để tìm kiếm những phương pháp và chiến thuật mới:
- Phương sai là một tham số quan trọng trong phân bổ tài sản đầu tư, được sử dụng cùng với hệ số tương quan, xác định phương sai của tài sản có thể giúp nhà đầu tư phát triển danh mục đầu tư nhằm tối ưu hóa sự đánh đổi giữa rủi ro và lợi nhuận.
Tìm hiểu ngay ma trận hệ số tương quan là gì? và cách tính nhé!
- Tuy nhiên, rủi ro hoặc biến động thường được thể hiện dưới dạng độ lệch chuẩn thay vì phương sai bởi vì nó dễ hiểu hơn.
Ví dụ:
Giả sử lợi nhuận cổ phiếu của bạn là 10% trong khoản đầu tư năm đầu tiên, 20% trong năm thứ hai và 15% trong năm thứ ba. Lợi nhuận trung bình là 15%.
Năm thứ nhất: Lợi nhuận = 10% – 15% = -5% | Lợi tức trung bình = -5% ² = 25%
Năm thứ hai: Lợi nhuận = 20% – 15% = 5% | Lợi tức trung bình 5% ² = 25%
Năm thứ ba: Lợi nhuận = 15% – 15% = 0% | Lợi tức trung bình 0% ² = 0
Đến đây ta trung bình cộng 3 năm: (25% + 25% + 0%)/3 = 16,667%.
Vậy theo ví dụ này thì phương sai của lợi nhuận cổ phiếu gần như là 17%.
Tương tự phương sai thì độ lệch chuẩn – standard deviation cũng có ứng dụng trong đầu tư đặc biệt là đầu tư tài chính nhé các bạn.
Tham khảo thêm phương sai sai số thay đổi là gì trong bài viết chuyên mục Stata của Mosl nhé!
6.Kết luận
Tổng hợp lại các mục MOSL đã cung cấp đến độc giả gồm:
- Khái niệm phương sai là gì?
- Vai trò phương sai là gì?
- Công thức tính phương sai là gì? Bonus thêm công thức tính độ lệch chuẩn – std deviation và khái niệm.
- Thuộc tính của phương sai là gì?
- Liệt kê các loại phương sai
- Ưu và nhược điểm phương sai là gì?
- Phương sai tổng thể và phương sai mẫu
- Phương sai áp dụng trong thực tế
Đến đây, MOSL xin chúc các bạn học tập và làm việc hiệu quả!
Xem thêm: Dịch vụ xử lý số liệu và hỗ trợ chạy Stata của Mosl.vn
