Chưa có sản phẩm trong giỏ hàng!
So sánh trung bình T-test trong SPSS: Độc lập vs Ghép cặp

Bạn từng đâu đó trước bảng số liệu SPSS cảm thấy bối rối chưa? Đặc biệt khi cần so sánh trung bình giữa hai nhóm, việc chọn đúng phương pháp kiểm định có thể khiến nhiều sinh viên và nhà nghiên cứu đau đầu. T-test là một trong những phương pháp thống kê cơ bản nhất, nhưng lại đóng vai trò then chốt trong phân tích dữ liệu nghiên cứu khoa học.
Tại Việt Nam, SPSS đã trở thành công cụ phân tích dữ liệu phổ biến trong các trường đại học và viện nghiên cứu. Theo thống kê của Bộ Giáo dục và Đào tạo, hơn 90% các chương trình đào tạo thạc sĩ yêu cầu sinh viên có kỹ năng sử dụng phần mềm thống kê chuyên nghiệp. Trong đó, SPSS chiếm ưu thế với giao diện thân thiện và khả năng xử lý đa dạng các loại dữ liệu.
MOSL hiểu rằng việc làm chủ T-test không chỉ giúp bạn hoàn thành luận văn tốt nghiệp mà còn là nền tảng vững chắc cho sự nghiệp nghiên cứu. Qua hàng ngàn ca tư vấn phân tích dữ liệu, chúng tôi nhận thấy nhiều học viên gặp khó khăn trong việc phân biệt khi nào nên sử dụng Independent Samples T-test và khi nào áp dụng Paired Samples T-test.
Bài viết này sẽ hướng dẫn bạn từng bước thực hiện cả hai loại kiểm định, từ việc chuẩn bị dữ liệu đến giải thích kết quả. Chúng ta sẽ khám phá những ví dụ thực tế từ nghiên cứu giáo dục và y học tại Việt Nam, đồng thời tìm hiểu cách đọc và báo cáo kết quả theo chuẩn khoa học quốc tế.
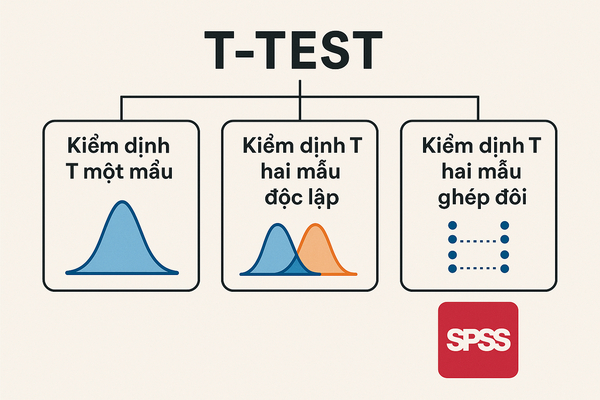
1. T-test trong SPSS là gì? Khái niệm cơ bản và phân loại
T-test là phương pháp kiểm định giả thuyết thống kê được sử dụng để so sánh giá trị trung bình. Bản chất của T-test dựa trên phân phối Student’s t, một phân phối xác suất được William Sealy Gosset phát triển đầu thế kỷ 20. Phương pháp này đặc biệt hiệu quả khi làm việc với mẫu nhỏ (n < 30) và độ lệch chuẩn tổng thể chưa biết.
Trong nghiên cứu khoa học, T-test giải quyết câu hỏi cốt lõi: “Sự khác biệt quan sát được giữa các nhóm có thực sự có ý nghĩa thống kê hay chỉ do ngẫu nhiên?” Đây chính là trái tim của suy luận thống kê – từ mẫu quan sát để rút ra kết luận về tổng thể lớn hơn.
| Loại T-test | Mục đích | Ví dụ thực tế |
|---|---|---|
| One-sample T-test | So sánh trung bình mẫu với một giá trị cố định | So sánh IQ trung bình của học sinh với chuẩn 100 |
| Independent Samples T-test | So sánh trung bình của hai nhóm độc lập | So sánh điểm thi giữa học sinh nam và nữ |
| Paired Samples T-test | So sánh hai bộ đo lường từ cùng nhóm đối tượng | So sánh điểm trước và sau khi học phương pháp mới |
Bài viết này tập trung vào hai loại T-test chính: Independent và Paired Samples. Cả hai đều thuộc nhóm kiểm định so sánh trung bình, nhưng áp dụng cho các thiết kế nghiên cứu khác nhau. Vehicle quan trọng là hiểu rõ khi nào nên sử dụng loại nào để tránh sai lầm trong phân tích.
Công thức toán học cơ bản của T-test có dạng: t = (trung bình quan sát – trung bình giả thuyết) / sai số chuẩn. Tuy nhiên, SPSS đã tự động hóa tất cả các phép tính phức tạp này, giúp người nghiên cứu tập trung vào việc hiểu và giải thích kết quả thay vì vướng mắc vào toán học.
1.1 Điều kiện tiên quyết khi sử dụng T-test
Trước khi thực hiện bất kỳ T-test nào, dữ liệu cần đáp ứng những giả định cơ bản. Đây không phải là các quy tắc cứng nhắc, mà là những điều kiện giúp kết quả kiểm định đáng tin cậy và có ý nghĩa thực tiễn.
Phân phối chuẩn là điều kiện đầu tiên. Biến phụ thuộc nên có phân phối xấp xỉ chuẩn trong từng nhóm. Với mẫu lớn (n > 30), Central Limit Theorem giúp nới lỏng giả định này. Tuy nhiên, với mẫu nhỏ, việc kiểm tra tính chuẩn trở nên quan trọng hơn.
Trong SPSS, bạn có thể kiểm tra phân phối chuẩn bằng Shapiro-Wilk test (cho mẫu < 50) hoặc Kolmogorov-Smirnov test (cho mẫu lớn hơn). Ngoài ra, biểu đồ histogram và Q-Q plot cũng cung cấp đánh giá trực quan về tính chuẩn của dữ liệu.
Tính độc lập của quan sát đảm bảo rằng giá trị của một quan sát không ảnh hưởng đến giá trị của quan sát khác. Điều này liên quan trực tiếp đến thiết kế nghiên cứu và cách thu thập dữ liệu. Ví dụ, nếu bạn khảo sát học sinh trong cùng lớp về cùng một đề tài, có thể xảy ra hiện tượng “cluster effect” – học sinh ảnh hưởng lẫn nhau.
Đối với Independent Samples T-test, giả định phương sai đồng nhất (homogeneity of variance) cần được kiểm tra. Levene’s test trong SPSS tự động thực hiện kiểm định này. Nếu phương sai không đồng nhất, SPSS cung cấp phiên bản hiệu chỉnh Welch’s t-test có độ tin cậy cao hơn.
Việc xử lý dữ liệu trong SPSS đòi hỏi sự cẩn thận từ khâu nhập liệu đến kiểm tra các giả định. Nhiều nghiên cứu không đạt yêu cầu đăng trên tạp chí quốc tế vì bỏ qua những bước kiểm tra cơ bản này.
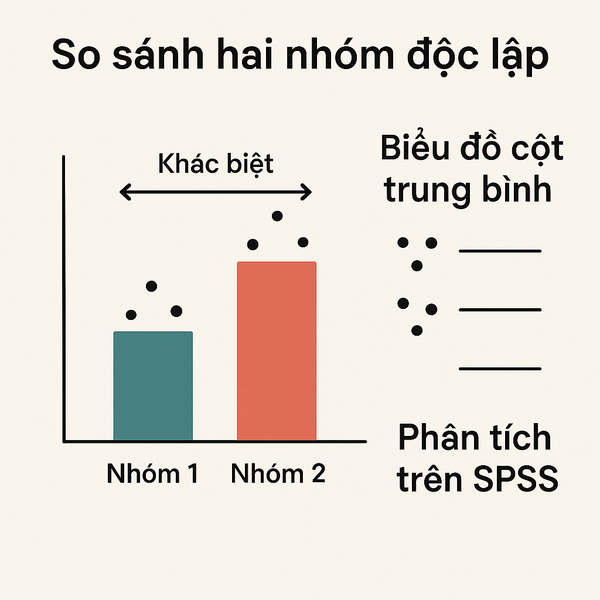
2. Independent Samples T-test: Phân tích so sánh hai nhóm độc lập
Independent Samples T-test được thiết kế để so sánh trung bình của hai nhóm hoàn toàn độc lập nhau. “Độc lập” có nghĩa là việc chọn một cá thể vào nhóm này không ảnh hưởng đến xác suất chọn bất kỳ cá thể nào vào nhóm kia. Đây là phương pháp phân tích phổ biến nhất trong nghiên cứu so sánh.
Trong một nghiên cứu giáo dục tại Đại học Quốc gia Hà Nội, nhóm nghiên cứu muốn so sánh hiệu quả học tập giữa học sinh nam và nữ trong môn Toán. Họ thu thập điểm cuối kỳ của 200 học sinh (100 nam, 100 nữ) từ 10 lớp khác nhau. Đây là trường hợp điển hình cho Independent Samples T-test vì giới tính là biến phân loại tự nhiên, không thể thay đổi.
Giả thuyết thống kê được thiết lập rõ ràng:
- H₀ (Null hypothesis): μ₁ = μ₂ (không có sự khác biệt về điểm trung bình giữa nam và nữ)
- H₁ (Alternative hypothesis): μ₁ ≠ μ₂ (có sự khác biệt có ý nghĩa thống kê)
Independent T-test có thể thực hiện theo hai hướng: kiểm định một phía (one-tailed) nếu bạn có giả thuyết định hướng về nhóm nào cao hơn, hoặc kiểm định hai phía (two-tailed) để phát hiện bất kỳ sự khác biệt nào. Hầu hết các nghiên cứu sử dụng kiểm định hai phía vì tính khách quan cao hơn.
Ưu điểm của phương pháp này bao gồm tính đơn giản trong thực hiện và giải thích kết quả. Kết quả dễ hiểu ngay cả với người không chuyên về thống kê. Phương pháp này cũng phù hợp với nhiều thiết kế nghiên cứu thực nghiệm và quan sát.
Nhược điểm chính là yêu cầu mẫu lớn hơn để đạt statistical power tương tự Paired T-test. Nguyên nhân là Independent T-test không kiểm soát được sự khác biệt cá thể giữa các nhóm, dẫn đến noise cao hơn trong dữ liệu.
2.1 Hướng dẫn thực hiện Independent Samples T-test trên SPSS từng bước
Chuẩn bị dữ liệu trong SPSS đòi hỏi cấu trúc đặc biệt. Bạn cần ít nhất hai biến: một biến phân loại (grouping variable) xác định nhóm, và một biến liên tục (test variable) chứa giá trị cần so sánh. Ví dụ, cột “Gioitinh” với giá trị 1=Nam, 2=Nữ, và cột “DiemToan” chứa điểm số.
Việc nhập dữ liệu vào SPSS cần tuân theo nguyên tắc “mỗi hàng là một quan sát, mỗi cột là một biến”. Điều này khác với cách tổ chức dữ liệu trong Excel thông thường, nơi mọi người thường tạo các cột riêng cho từng nhóm.
Bước 1: Truy cập menu phân tích
Từ menu chính, chọn Analyze → Compare Means → Independent-Samples T Test. Giao diện SPSS 29.0 đã được cải tiến với icons rõ ràng hơn và tooltip hữu ích cho từng tùy chọn.
Bước 2: Thiết lập biến
Di chuyển biến số (ví dụ: Diem_Toan) vào ô “Test Variable(s)”. Đây là biến mà bạn muốn so sánh trung bình. Một phân tích có thể chứa nhiều test variables cùng lúc, SPSS sẽ tự động chạy từng phân tích riêng biệt.
Biến phân nhóm (ví dụ: Gioi_tinh) được đưa vào ô “Grouping Variable”. Lưu ý rằng SPSS sẽ hiển thị dấu hỏi chấm sau tên biến, yêu cầu bạn định nghĩa các nhóm cụ thể.
Bước 3: Định nghĩa nhóm
Click vào nút “Define Groups”. Có hai tùy chọn:
- “Use specified values”: Nhập mã cụ thể cho từng nhóm (ví dụ: Group 1 = 1, Group 2 = 2)
- “Cut point”: SPSS sẽ tự động chia dữ liệu dựa trên một giá trị ngưỡng
Đối với dữ liệu giới tính được mã hóa 1 và 2, chọn tùy chọn đầu và nhập 1 cho Group 1, 2 cho Group 2.
Bước 4: Tùy chọn bổ sung
Click “Options” để thiết lập mức độ tin cậy (confidence interval) và cách xử lý missing values. Mặc định 95% CI phù hợp với hầu hết nghiên cứu. “Exclude cases analysis by analysis” được khuyến nghị khi có nhiều test variables.
Bước 5: Chạy phân tích
Click “OK” để thực hiện phân tích. SPSS sẽ tự động tạo output trong cửa sổ riêng, bao gồm bảng thống kê mô tả và kết quả kiểm định.
2.2 Đọc và phân tích kết quả Independent Samples T-test
Output của SPSS cho Independent T-test bao gồm hai bảng chính, mỗi bảng mang thông tin quan trọng cho việc giải thích kết quả. Hiểu đúng cách đọc những bảng này là chìa khóa để viết báo cáo nghiên cứu chính xác và thuyết phục.
Bảng Group Statistics
cung cấp thống kê mô tả cơ bản cho từng nhóm. Bảng này bao gồm số lượng quan sát (N), trung bình (Mean), độ lệch chuẩn (Std. Deviation), và sai số chuẩn của trung bình (Std. Error Mean) cho mỗi nhóm.
Ví dụ kết quả:
- Nam (N=100): Mean = 7.45, SD = 1.23
- Nữ (N=100): Mean = 7.89, SD = 1.15
Từ những số liệu này, ta thấy điểm trung bình của nữ cao hơn nam 0.44 điểm, với độ lệch chuẩn tương đương nhau. Tuy nhiên, câu hỏi quan trọng là sự khác biệt này có ý nghĩa thống kê hay không.
Bảng Independent Samples Test chứa trái tim của phân tích. Bảng này được chia thành hai phần chính: Levene’s Test for Equality of Variances và T-test for Equality of Means.
Levene’s test kiểm tra giả định về phương sai đồng nhất với giả thuyết:
- H₀: σ₁² = σ₂² (phương sai của hai nhóm bằng nhau)
- H₁: σ₁² ≠ σ₂² (phương sai khác nhau)
Nếu Sig. của Levene’s test > 0.05, chúng ta chấp nhận H₀ và sử dụng kết quả “Equal variances assumed”. Ngược lại, sử dụng “Equal variances not assumed” (Welch’s t-test).
Phần T-test bao gồm các thông số quan trọng:
- t-value: Giá trị t tính toán (-2.657 trong ví dụ)
- df: Bậc tự do (198 cho equal variances assumed)
- Sig. (2-tailed): Giá trị p-value (0.008)
- Mean Difference: Sự khác biệt trung bình (-0.44)
- 95% Confidence Interval: Khoảng tin cậy của sự khác biệt
Cách báo cáo kết quả theo chuẩn APA:
“Một Independent Samples T-test được thực hiện để so sánh điểm Toán giữa học sinh nam và nữ. Kết quả cho thấy có sự khác biệt có ý nghĩa thống kê giữa điểm số của nam (M = 7.45, SD = 1.23) và nữ (M = 7.89, SD = 1.15); t(198) = -2.657, p = 0.008, Cohen’s d = 0.37. Học sinh nữ có điểm trung bình cao hơn học sinh nam 0.44 điểm.”
Cohen’s d đo lường effect size (độ lớn hiệu ứng) được tính bằng công thức: d = (Mean1 – Mean2) / Pooled Standard Deviation. Giá trị này giúp đánh giá ý nghĩa thực tiễn của sự khác biệt:
- d = 0.2: Effect size nhỏ
- d = 0.5: Effect size trung bình
- d = 0.8: Effect size lớn
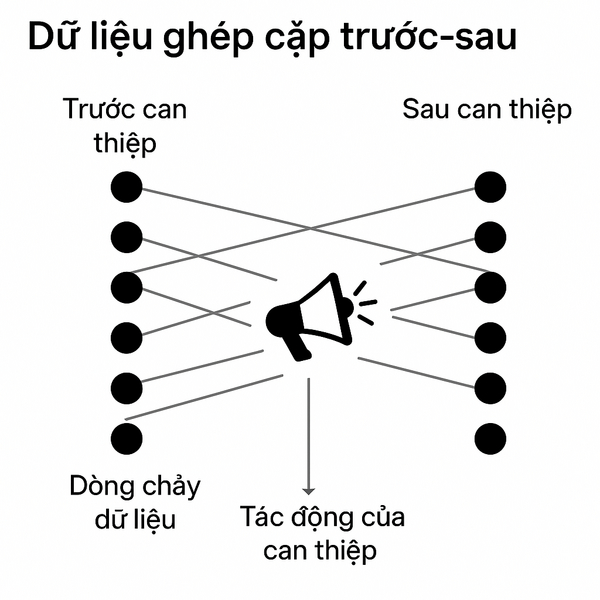
3. Paired Samples T-test: Phân tích dữ liệu ghép cặp
Paired Samples T-test được thiết kế cho những tình huống nghiên cứu đặc biệt, nơi chúng ta so sánh hai đo lường từ cùng một nhóm đối tượng. Điều này tạo ra một thiết kế nghiên cứu mạnh mẽ hơn vì mỗi đối tượng trở thành “control” cho chính mình, loại bỏ nhiều yếu tố gây nhiễu.
Tưởng tượng bạn là giảng viên tại Học viện Nông nghiệp Việt Nam, muốn đánh giá hiệu quả của phương pháp dạy học mới. Thay vì chia lớp thành hai nhóm (một nhóm học theo phương pháp cũ, một nhóm học theo phương pháp mới), bạn cho cả lớp làm bài kiểm tra trước khi học (pre-test), sau đó áp dụng phương pháp mới và cho làm bài kiểm tra tương tự sau khóa học (post-test).
Ưu điểm vượt trội của Paired T-test nằm ở khả năng kiểm soát các biến confounding. Khi so sánh điểm pre-test và post-test của cùng một học sinh, các yếu tố như trí thông minh, background kiến thức, động lực học tập đều được “cố định”. Điều này giúp tăng statistical power đáng kể – khả năng phát hiện sự khác biệt thực sự khi nó tồn tại.
Một nghiên cứu tại Bệnh viện Việt Đức so sánh hiệu quả của phương pháp điều trị mới đối với huyết áp. Thay vì có nhóm đối chứng riêng, họ đo huyết áp của 50 bệnh nhân trước điều trị, sau đó đo lại sau 4 tuần điều trị. Mỗi bệnh nhân trở thành control cho chính mình, loại bỏ ảnh hưởng của tuổi tác, giới tính, và các yếu tố di truyền.
Thiết kế nghiên cứu Paired T-test có thể áp dụng trong nhiều tình huống:
- Before-After studies: Đo lường trước và sau can thiệp
- Matched pairs: Ghép cặp đối tượng theo các tiêu chí cụ thể
- Repeated measures: Đo lường lặp lại trên cùng đối tượng
Đặc điểm quan trọng là thứ tự ghép đôi phải có ý nghĩa. Điểm pre-test của học sinh A phải được ghép với đi
ểm post-test của chính học sinh A, không phải của học sinh khác.
Công thức toán học của Paired T-test dựa trên trung bình difference scores: t = d̄ / (sd/√n), trong đó d̄ là trung bình các hiệu số, sd là độ lệch chuẩn của các hiệu số, n là số cặp quan sát. SPSS tự động tính toán tất cả để bạn tập trung vào giải thích.
Nhược điểm cần lưu ý bao gồm khả năng có carry-over effects trong repeated measures designs. Nếu khoảng cách thời gian giữa hai lần đo quá ngắn, lần đo đầu có thể ảnh hưởng đến lần đo thứ hai. Ngoài ra, việc mất dữ liệu (missing data) nghiêm trọng hơn vì mất một quan sát đồng nghĩa với mất cả một cặp.
3.1 Hướng dẫn thực hiện Paired Samples T-test trên SPSS từng bước
Cấu trúc dữ liệu cho Pa
ired T-test khác biệt hoàn toàn so với Independent T-test. Thay vì có một biến phân nhóm, bạn cần hai cột riêng biệt cho hai lần đo. Ví dụ: cột “Pretest” chứa điểm kiểm tra đầu khóa và cột “Posttest” chứa điểm cuối khóa của cùng sinh viên.
Mỗi hàng trong dataset đại diện cho một đối tượng nghiên cứu, với hai giá trị được đo từ đối tượng đó. Điều này khác hẳn với cấu trúc long-format thường thấy trong các phân tích khác.
Bước 1: Chuẩn bị và kiểm tra dữ liệu
Trước khi phân tích, kiểm tra tính hoàn chỉnh của cặp dữ liệu. SPSS sẽ tự động loại bỏ những trường hợp thiếu dữ liệu ở một trong hai biến, có thể làm giảm sample size đáng kể.
Kiểm tra outliers bằng cách tạo biến difference = Posttest – Pretest, sau đó vẽ boxplot. Những giá trị nằm ngoài 1.5 IQR có thể là outliers cần xem xét.
Bước 2: Truy cập menu Paired-Samples T Test
Từ menu chính SPSS, chọn Analyze → Compare Means → Paired-Samples T Test. Giao diện này đơn giản hơn Independent T-test vì không cần định nghĩa nhóm.
Bước 3: Chọn cặp biến để phân tích
Trong danh sách biến bên trái, highlight hai biến cần so sánh (ví dụ: Pretest và Posttest). Click mũi tên để chuyển cả hai biến vào ô “Paired Variables”. SPSS sẽ tự động ghép chúng thành “Pair 1”.
Bạn có thể thêm nhiều cặp biến cùng lúc nếu muốn thực hiện several paired tests trong một lần chạy. Mỗi cặp sẽ được phân tích độc lập.
Bước 4: Thiết lập tùy chọn
Click “Options” để thiết lập confidence interval (mặc định 95%) và cách xử lý missing values. “Exclude cases analysis by analysis” thường phù hợp nhất cho paired data.
Bước 5: Thực hiện phân tích
Click “OK” để chạy phân tích. SPSS sẽ tạo ra ba bảng output: Paired Samples Statistics, Paired Samples Correlations, và Paired Samples Test.
Quá trình này đơn giản hơn nhiều so với Independent T-test vì không cần lo lắng về việc kiểm tra equality of variances hay định nghĩa groups.
3.2 Đọc và phân tích kết quả Paired Samples T-test
Output của Paired Samples T-test trong SPSS cung cấp ba bảng thông tin, mỗi bảng đóng góp một góc nhìn quan trọng về dữ liệu và kết quả phân tích.
Bảng Paired Samples Statistics hiển thị thống kê mô tả cơ bản cho cả hai lần đo. Bảng này bao gồm Mean, N, Std. Deviation, và Std. Error Mean cho mỗi biến trong cặp.
Ví dụ kết quả:
- Pre_test: Mean = 6.85, N = 45, SD = 1.67
- Post_test: Mean = 7.41, N = 45, SD = 1.52
Từ bảng này, ta thấy có sự cải thiện từ 6.85 điểm lên 7.41 điểm (tăng 0.56 điểm). Câu hỏi quan trọng là liệu sự cải thiện này có ý nghĩa thống kê hay không.
Bảng Paired Samples Correlations cho biết mức độ tương quan giữa hai lần đo. Đây là thông tin quan trọng nhưng thường bị bỏ qua. Correlation cao (r > 0.7) cho thấy sự nhất quán trong thứ hạng của đối tượng giữa hai lần đo, tăng công suất thống kê của test.
Trong ví dụ này: r = 0.823, N = 45, Sig. = 0.000. Correlation cao này chứng minh việc sử dụng Paired T-test là phù hợp và hiệu quả hơn Independent T-test.
Bảng Paired Samples Test chứa kết quả chính của phân tích. Bảng này tập trung vào difference scores (các hiệu số) và kiểm định liệu trung bình của các hiệu số có khác 0 hay không.
Các thông số quan trọng bao gồm:
- Mean Difference: Trung bình của (Variable1 – Variable2) = -0.56
- Std. Deviation: Độ lệch chuẩn của các difference scores = 0.94
- t-value: Giá trị t tính toán = -3.947
- df: Degrees of freedom = N-1 = 44
- Sig. (2-tailed): P-value = 0.000
Effect Size calculation cho Paired T-test sử dụng Cohen’s d với công thức: d = Mean Difference / SD of differences = 0.56 / 0.94 = 0.595. Đây được coi là effect size “trung bình đến lớn” theo thang đo Cohen.
Mẫu báo cáo kết quả bằng tiếng Việt:
“Một Paired Samples T-test được thực hiện để đánh giá hiệu quả của phương pháp giảng dạy mới. Kết quả cho thấy có sự cải thiện có ý nghĩa thống kê từ điểm pre-test (M = 6.85, SD = 1.67) đến điểm post-test (M = 7.41, SD = 1.52); t(44) = -3.947, p < 0.001, Cohen’s d = 0.595. Phương pháp mới giúp cải thiện điểm số trung bình 0.56 điểm với effect size ở mức trung bình đến lớn.”
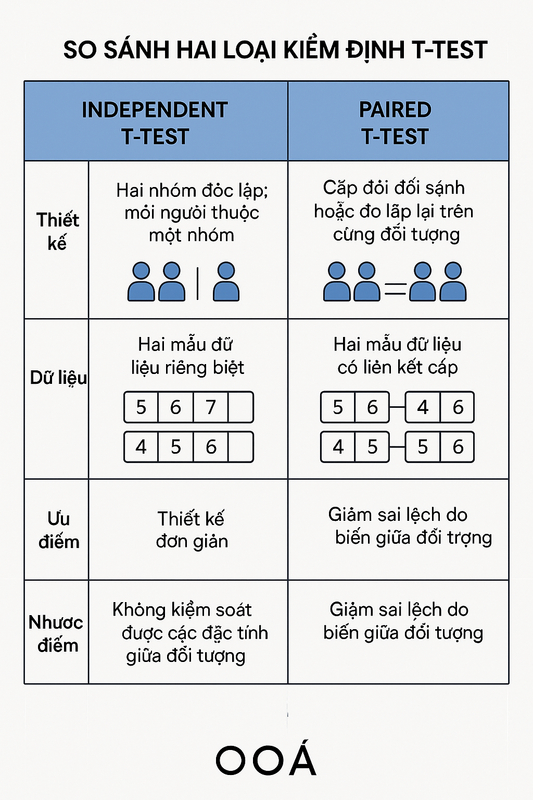
4. Bảng so sánh toàn diện: Independent vs Paired Samples T-test
Việc lựa chọn đúng loại T-te
st ảnh hưởng trực tiếp đến tính chính xác và giá trị của nghiên cứu. Hiểu sâu những điểm khác biệt giúp bạn đưa ra quyết định đúng đắn và tránh những sai lầm phổ biến trong phân tích dữ liệu.
| Tiêu chí so sánh | Independent Samples T-test | Paired Samples T-test |
|---|---|---|
| **Thiết kế nghiên cứu** | Hai nhóm độc lập, khác nhau | Cùng nhóm, hai thời điểm đo |
| **Cấu trúc dữ liệu** | 2 cột: scores + group codes | 2 cột: measurement1 + measurement2 |
| **Statistical Power** | Thấp hơn (nhiều variance) | Cao hơn (kiểm soát individual differences) |
| **Yêu cầu mẫu** | Lớn hơn để đạt power tương tự | Nhỏ hơn, hiệu quả hơn |
| **Menu SPSS** | Compare Means > Independent-Samples | Compare Means > Paired-Samples |
| **Giả định chính** | Equal variances (Levene’s test) | Normality of difference scores |
| **Xử lý missing data** | Mất một case, mất một quan sát | Mất một case, mất một cặp |
| **Ví dụ ứng dụng** | So sánh nam vs nữ, nhóm A vs B | Pre-test vs Post-test, Before vs After |
| **Effect size tính toán** | Cohen’s d = (M1-M2)/Pooled SD | Cohen’s d = Mean diff/SD of differences |
| **Khả năng causality** | Khó khẳng định nhân quả | Mạnh hơn về mối liên hệ nhân quả |
Flowchart ra quyết định giúp lựa chọn phương pháp phù hợp:
- Bạn có hai nhóm đối tượng khác nhau? → Yes: Independent T-test
- Bạn có cùng nhóm đối tượng được đo 2 lần? → Yes: Paired T-test
- Bạn có thể ghép cặp đối tượng theo tiêu chí cụ thể? → Yes: Paired T-test
- Các nhóm hoàn toàn độc lập và không thể ghép cặp? → Yes: Independent T-test
Trong thực tế nghiên cứu tại Việt Nam, Independent T-test thường được sử dụng trong các nghiên cứu cắt ngang (cross-sectional studies) so sánh các nhóm dân số khác nhau. Paired T-test phổ biến trong nghiên cứu can thiệp và đánh giá hiệu quả điều trị.
5. Ví dụ thực tế: Phân tích dữ liệu bằng SPSS từ A đến Z
Để minh họa cụ thể, chúng ta sẽ thực hiện hai ví dụ hoàn chỉnh từ raw data đến kết luận cuối cùng. Những ví dụ này dựa trên các tình huống thực tế trong nghiên cứu giáo dục và y tế tại Việt Nam.
5.1 Ví dụ 1: Independent Samples T-test – So sánh điểm toán giữa học sinh nam và nữ
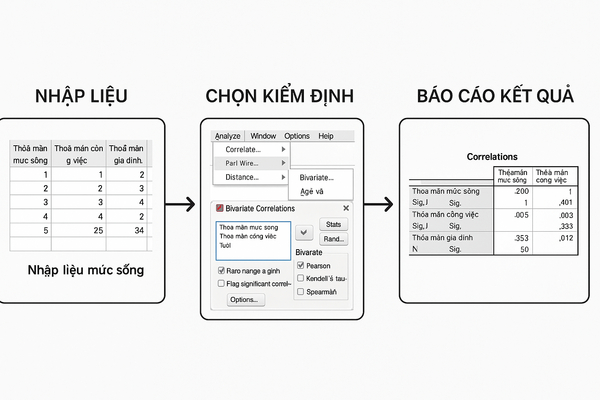
Bối cảnh: Trường THPT Nguyễn Tất Thành, Hà Nội muốn đánh giá xem có sự khác biệt về năng lực toán học giữa học sinh nam và nữ hay không. Họ lấy mẫu ngẫu nhiên 80 học sinh lớp 11 (40 nam, 40 nữ) và ghi nhận điểm kiểm tra 15 phút môn Toán.
Dữ liệu mẫu:
ID | Gioi_tinh | Diem_Toan
1 | 1 | 7.5
2 | 2 | 8.2
3 | 1 | 6.8
... (80 quan sát)
Bước 1: Khám phá dữ liệu
Trước khi thực hiện T-test, sử dụng Explore procedure trong SPSS để kiểm tra phân phối và phát hiện outliers. Chọn Analyze → Descriptive Statistics → Explore, đưa DiemToan vào Dependent và Gioitinh vào Factor.
Kết quả cho thấy:
- Nhóm nam: Mean = 7.23, SD = 1.45, Median = 7.30 (phân phối gần chuẩn)
- Nhóm nữ: Mean = 7.68, SD = 1.38, Median = 7.70 (phân phối gần chuẩn)
Bước 2: Kiểm tra giả định
Shapiro-Wilk test trong Explore cho thấy p > 0.05 cho cả hai nhóm, xác nhận phân phối chuẩn. Không có outliers nghiêm trọng được phát hiện.
Bước 3: Thực hiện Independent T-test
Analyze → Compare Means → Independent-Samples T Test
- Test Variable: Diem_Toan
- Grouping Variable: Gioi_tinh (Define Groups: 1, 2)
Kết quả:
Levene’s Test: F = 0.182, p = 0.671 → Assumption of equal variance được thỏa mãn
T-test results (Equal variances assumed):
- t = -1.437
- df = 78
- p = 0.155
- Mean Difference = -0.45
- 95% CI: [-1.08, 0.18]
Giải thích và kết luận:
Không có sự khác biệt có ý nghĩa thống kê về điểm toán giữa học sinh nam (M = 7.23, SD = 1.45) và nữ (M = 7.68, SD = 1.38); t(78) = -1.437, p = 0.155. Mặc dù học sinh nữ có điểm trung bình cao hơn 0.45 điểm, sự khác biệt này có thể do ngẫu nhiên.
5.2 Ví dụ 2: Paired Samples T-test – Đánh giá hiệu quả chương trình đào tạo
Bối cảnh: Trung tâm Ngoại ngữ HUST muốn đánh giá hiệu quả khóa học IELTS cấp tốc trong 3 tháng. Họ cho 35 học viên làm bài test đầu vào, sau đó học 3 tháng và làm bài test tương tự.
Dữ liệu mẫu:
ID | Pre_IELTS | Post_IELTS
1 | 5.5 | 6.0
2 | 4.0 | 5.5
3 | 6.0 | 6.5
... (35 quan sát)
Bước 1: Tạo difference variable
Transform → Compute Variable: tạo biến “Improvement = PostIELTS – PreIELTS” để dễ dàng kiểm tra outliers và tính chuẩn.
Bước 2: Khám phá distribution of differences
Improvement: Mean = 0.67, SD = 0.52, Min = -0.5, Max = 1.5
Histogram cho thấy phân phối gần chuẩn, không có outliers nghiêm trọng.
Bước 3: Thực hiện Paired T-test
Analyze → Compare Means → Paired-Samples T Test
- Pair 1: PreIELTS with PostIELTS
Kết quả:
Paired Samples Statistics:
- Pre_IELTS: M = 5.24, N = 35, SD = 0.89
- Post_IELTS: M = 5.91, N = 35, SD = 0.94
Paired Samples Correlations:
- r = 0.856, p < 0.001 (correlation cao, phù hợp cho paired design)
Paired Samples Test:
- Mean Difference = -0.67
- t = -7.582
- df = 34
- p < 0.001
- Cohen’s d = 0.67/0.52 = 1.29 (large effect size)
Giải thích và kết luận:
Có sự cải thiện có ý nghĩa thống kê từ điểm pre-test (M = 5.24, SD = 0.89) đến post-test (M = 5.91, SD = 0.94); t(34) = -7.582, p < 0.001, Cohen’s d = 1.29. Khóa học giúp cải thiện điểm IELTS trung bình 0.67 điểm với effect size lớn.
Common mistakes và cách tránh:
Nhiều người nhầm lẫn giữa correlation trong Paired Samples với causation. Correlation cao (0.856) chỉ cho thấy ranking consistency, không chứng minh intervention gây ra improvement. Để khẳng định causality, cần thiết kế controlled study với comparison group.
6. Những lỗi thường gặp khi thực hiện T-test trong SPSS
Qua kinh nghiệm tư vấn hàng ngàn trường hợp phân tích dữ liệu, MOSL nhận thấy những lỗi phổ biến mà người nghiên cứu thường mắc phải. Hiểu và tránh những lỗi này giúp đảm bảo tính chính xác của nghiên cứu.

6.1 Lỗi về chuẩn bị dữ liệu
Lỗi format dữ liệu là nguyên nhân hàng đầu gây sai kết quả. Nhiều người nhập dữ liệu từ Excel vào SPSS theo cách không đúng chuẩn. Với Independent T-test, dữ liệu phải ở dạng “long format” – mỗi hàng là một quan sát, không phải “wide format” với các nhóm ở cột riêng.
Ví dụ sai:
| Nam_1 | Nam_2 | ... | Nu_1 | Nu_2 | ... |
|-------|--------|-----|------|------|-----|
| 7.5 | 8.1 | ... | 7.8 | 8.3 | ... |
Cách đúng:
| ID | Gioi_tinh | Diem |
|----|-----------|------|
| 1 | 1 | 7.5 |
| 2 | 1 | 8.1 |
| 3 | 2 | 7.8 |
Missing value handling cũng gây nhiều nhầm lẫn. SPSS có several options: exclude cases pairwise vs listwise. Với Paired T-test, việc mất data ở một trong hai variables sẽ loại bỏ toàn bộ case, có thể giảm sample size nghiêm trọng.
Outliers detection quan trọng nhưng thường bị bỏ qua. Một outlier có thể skew kết quả đáng kể với sample size nhỏ. Những giá trị cách trung bình hơn 2.5-3 standard deviations nên được investigate kỹ lưỡng.
6.2 Lỗi về thực hiện kiểm định
Chọn sai loại T-test xảy ra phổ biến. Nhiều người sử dụng Independent T-test cho dữ liệu paired, hoặc ngược lại. Câu hỏi quyết định: “Có phải cùng một đối tượng được đo nhiều lần không?” Nếu có, dùng Paired; nếu không, dùng Independent.
Vi phạm assumptions mà không kiểm tra là lỗi nghiêm trọng. Với Independent T-test, Levene’s test kiểm tra equal variances. Nếu p < 0.05, phải sử dụng Welch’s t-test (equal variances not assumed). SPSS tự động cung cấp cả hai kết quả, nhưng người dùng cần biết chọn đúng.
One-tailed vs Two-tailed confusion cũng khá thường gặp. Mặc định SPSS báo cáo two-tailed p-value. Nếu bạn có directional hypothesis và muốn one-tailed test, chia p-value cho 2. Tuy nhiên, most journals ưa chuộng two-tailed tests vì tính conservative.
6.3 Lỗi về giải thích kết quả
P-hacking là công việc thao túng phân tích để đạt p < 0,05. Ví dụ: loại bỏ các ngoại lệ một cách có chọn lọc, thay đổi tiêu chí nhóm hoặc thử nhiều phân tích cho đến khi tìm thấy ý nghĩa. Đây là hành vi sai trái nghiêm trọng trong nghiên cứu.
Nhầm lẫn giữa ý nghĩa thống kê và ý nghĩa thực tế rất phổ biến. P-value nhỏ không đồng nghĩa với phát hiện quan trọng. Kích thước hiệu ứng mới được xác thực cho biết mức độ khác biệt. Ví dụ: với cỡ mẫu rất lớn, chênh lệch 0,01 điểm có thể có ý nghĩa (p < 0,05) nhưng không có ý nghĩa thực tế.
Việc giải thích sai về khoảng tin cậy cũng thường thấy. CI 95% của sự khác biệt trung bình không có nghĩa là “có sự khác biệt về dân số xác thực 95% nằm trong khoảng này”. Giải thích đúng: “Nếu lặp lại nghiên cứu nhiều lần, 95% số TCTD sẽ chứa sự khác biệt thực sự về quần thể.”
Khái quát hóa quá mức từ các phát hiện mẫu đã hát dân số rộng hơn thiết kế được phép. Nếu nghiên cứu chỉ bao gồm sinh viên từ một trường đại học, không thể khái quát hóa kết quả cho tất cả sinh viên Việt Nam.
7. Kiểm định thay thế khi vi phạm giả định T-test
Khi dữ liệu không đáp ứng các giả định của T-test, việc áp dụng các thử nghiệm tham số chậm có thể dẫn đến kết luận sai lệch. May mắn thay, tài liệu thống kê cung cấp nhiều phương pháp tiếp cận mạnh mẽ và đáng tin cậy.
Kiểm định Mann-Whitney U (còn gọi là kiểm định tổng xếp hạng Wilcoxon) thay thế Kiểm định T độc lập khi dữ liệu không có phân phối chuẩn. Thay vì so sánh các phương tiện, bài kiểm tra này so sánh các trung vị và thứ hạng của các quan sát. Đặc biệt hữu ích với dữ liệu thứ tự hoặc dữ liệu liên tục có phân phối sai lệch.
Trong SPSS: Phân tích → Kiểm tra không tham số → Mẫu độc lập, chọn Mann-Whitney U. Kiểm tra này không yêu cầu phân phối chuẩn nhưng vẫn giả định tính độc lập và phân bố hình dạng tương tự giữa các nhóm.
Bài kiểm tra Xếp hạng có chữ ký của Wilcoxon tương đương với bài kiểm tra T theo cặp. Hữu ích khi điểm chênh lệch không được phân phối bình thường. Thử nghiệm tập trung vào cường độ và hướng thay đổi, không giả định hình dạng phân phối cụ thể.
Đường dẫn SPSS: Analyze → Nonparametric Tests → Related Samples, chọn Wilcoxon signed-rank test. Đặc biệt phù hợp với dữ liệu thang đo Likert trong nghiên cứu tâm lý.
Các phương pháp Bootstrap đang trở nên phổ biến như một giải pháp thay thế mạnh mẽ. Bootstrap resampling tạo ra hàng nghìn ước tính mẫu từ dữ liệu gốc, cung cấp phân phối thực nghiệm mà không có giả định phân phối. SPSS Extension Bundles có các tùy chọn bootstrap cho hầu hết các bài kiểm tra thống kê.
Các bài kiểm tra t mạnh mẽ như Welch’s t-test (unequal variances) tự động có trong đầu ra SPSS. Bài kiểm tra trung bình cắt tỉa của Yuen cũng là một lựa chọn tốt cho dữ liệu chuẩn bị nhiễm với các giá trị ngoại lai.
8. Kết luận
T-test là nền tảng vững chắc trong kê dữ liệu phân tích chủ hoạt động. Qua những ví dụ thực tế và hướng dẫn chi tiết, chúng tôi đã khám phá ra sức mạnh của cả T-test Mẫu Độc lập và Cặp đôi trong công việc trả lời những câu hỏi nghiên cứu quan trọng.
Điều quan trọng nhất không phải là ghi nhớ các bước thao tác mà là hiểu sâu về logic đằng sau mỗi phương pháp. T-test độc lập giúp so sánh các nhóm khác nhau, trong khi T-test cặp đôi tận dụng sức mạnh của thiết kế bên trong đối tượng để đạt được sức mạnh thống kê cao hơn kích thước mẫu nhỏ hơn.
SPSS đã đơn giản hóa đáng kể độ phức tạp tính toán, cho phép chúng ta tập trung vào công việc đặt câu hỏi đúng, thiết kế nghiên cứu phù hợp, và giải quyết kết quả theo cách có ý nghĩa. Tuy nhiên, phần mềm chỉ là công cụ – sự hiểu biết về tư duy thống kê mới là chìa khóa thực sự.
Trong bối cảnh nghiên cứu khoa học ngày càng đòi hỏi tính chất nghiêm trọng và chính xác, nắm chắc các phương pháp thống kê cơ bản như T-test không chỉ giúp hoàn thành luận văn mà còn xây dựng nền tảng vững chắc cho sự nghiệp nghiên cứu dài hạng.
Liên hệ ngay cho MOSL để nhận thông tin tư vấn bằng cách liên hệ Hotline/Zalo: 0707339698. Đội ngũ chuyên gia của chúng tôi sẵn sàng hỗ trợ bạn từ việc thiết kế nghiên cứu, phân tích dữ liệu, đến viết báo cáo kết quả theo chuẩn quốc tế.
Để theo dõi thêm nhiều kiến thức bổ ích về phân tích dữ liệu và phương pháp nghiên cứu, hãy kết nối với chúng tôi tại Facebook MOSL Group, nơi chia sẻ những insights mới nhất từ cộng đồng nghiên cứu khoa học.
Các câu hỏi thường được quan tâm bao gồm:
Khi nào nên sử dụng T-test độc lập thay vì T-test được ghép nối? T-test độc lập được sử dụng khi so sánh hai nhóm đối tượng khác nhau, trong khi T-test cặp đôi dành cho cùng một nhóm đối tượng được đo lường ở hai thời điểm khác nhau.
Làm sao biết dữ liệu có chuẩn phân phối vi phạm? Sử dụng Shapiro-Wilk test cho mẫu nhỏ (n<50) hoặc Kolmogorov-Smirnov test cho mẫu lớn. Nếu p-value < 0,05, dữ liệu không được phân phối chuẩn.
Kích thước hiệu ứng quan trọng như thế nào? Kích thước hiệu ứng đo lường độ lớn của sự khác biệt, quan trọng hơn giá trị p trong việc đánh giá ý nghĩa thực tế. Cohen’s d = 0,2 (nhỏ), 0,5 (trung bình), 0,8 (lớn).
Có thể so sánh hơn 2 nhóm bằng T-test không? Không, T-test chỉ dành cho 2 nhóm. Để so sánh 3+ nhóm, hãy sử dụng ANOVA để tránh vấn đề so sánh nhiều lần.
Cách xử lý các ngoại lệ trong T-test? Đầu tiên hãy điều tra các ngoại lệ để xác định có phải lỗi nhập dữ liệu hay không. Nếu là dữ liệu hợp pháp, có thể sử dụng các lựa chọn thay thế mạnh mẽ như T-test đã khởi động.
T-test được ghép nối có yêu cầu kích thước mẫu tối thiểu? Không có mức độ cứng tối thiểu nhưng nhìn chung n ≥ 20 cho đủ công suất. Với các mẫu nhỏ hơn, hãy xem xét các lựa chọn thay thế không tham số.
Tài liệu tham khảo từ các nguồn uy tín:
American Psychological Association – Statistical Methods Guidelines cho chuẩn báo cáo APA.
Cohen, J. (1988) Statistical Power Analysis for the Behavioral Sciences cho hiểu biết về effect sizes.
Field, A. Discovering Statistics Using SPSS cho hướng dẫn practical implementation.
IBM SPSS Statistics Documentation cho technical specifications và updates.
Journal of Statistical Education cho pedagogical approaches trong teaching statistics.
Các thuật ngữ liên quan cần biết:
Statistical Power – Khả năng phát hiện hiệu ứng thực sự khi nó tồn tại, thường là ≥ 0,80.
Lỗi loại I – Bác bỏ giả thuyết vô hiệu khi nó đúng, được kiểm soát bởi mức α (thường là 0,05).
Lỗi loại II – Không bác bỏ được giả thuyết vô hiệu khi thay thế đúng, được kiểm soát bởi β.
Khoảng tin cậy – Phạm vi giá trị có khả năng chứa tham số quần thể.
Bậc tự do – Số lượng giá trị độc lập trong phép tính, ảnh hưởng đến hình dạng phân phối t.
Giá trị P – Xác suất quan sát kết quả ít nhất là cực trị nếu giả thuyết vô hiệu là đúng.